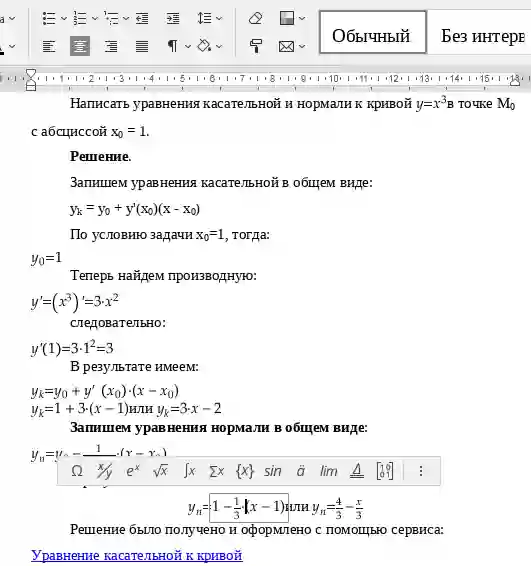
Уравнение касательной к кривой линии
Уравнение касательной в общем виде записывается как:yk=y0+y'(x0)(x-x0)
Назначение. Онлайн-калькулятор предназначен для нахождения уравнения касательной к графику функции. Решение оформляется в формате Word (см. пример).
Примеры:
Функция задана в явном виде, например y = 1/2*x3+5*x
Функция задана в неявном виде, например y2 - 1/2*x3 - 8
Функция задана в параметрическом виде, например x = 5*cos(t);y = 3*sin(t)
Функция задана в явном виде, например y = 1/2*x3+5*x
Функция задана в неявном виде, например y2 - 1/2*x3 - 8
Функция задана в параметрическом виде, например x = 5*cos(t);y = 3*sin(t)
Функция задана в явном виде:
Функция задана в неявном виде:
Функция задана в параметрическом виде:
Алгоритм составления уравнения касательной к графику функции
- Вычисление значения функции y0 в точке x0:y0 = f(x0). Если исходное значение y0 задано, то переходим к п.2.
- Нахождение производной y'(x).
- Вычисление значения производной при x0.
- Запись уравнения касательной к кривой линии в форме: yk = y0 + y'(y0)(x - x0)
Касательные к кривым второго порядка
| Уравнение линии | Уравнение касательной | |
| Эллипс | 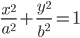 |
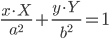 |
| Гипербола | 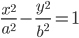 |
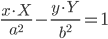 |
| Парабола | y2 = 2px | yY = p(X + x) |
см. также Касательная плоскость к поверхности.