Автокорреляция уровней временного ряда

Автокорреляция уровней ряда – корреляционная между последовательными уровнями одного и того же ряда динамики (сдвинутыми на определенный промежуток времени L – лаг). Автокорреляция может быть измерена коэффициентом автокорреляции.

Назначение сервиса. Онлайн-калькулятор позволит прямо на сайте бесплатно провести анализ уровней временного ряда y_t на наличие автокорреляции.

Инструкция. Укажите количество данных (количество строк). Полученное решение сохраняется в файле Word.

Скачать пример оформления

Лаг (сдвиг во времени) определяет порядок коэффициента автокорреляции. Если L = 1, то имеем коэффициент автокорреляции 1-го порядка r_t,t-1, если L = 2, то коэффициент автокорреляции 2-го порядка r_t,t-2 и т.д. Следует учитывать, что с увеличением лага на единицу число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается на 1. Поэтому обычно рекомендуют максимальный порядок коэффициента автокорреляции, равный n/4.
Рассчитав несколько коэффициентов автокорреляции, можно определить лаг (I), при котором автокорреляция (r_t,t-L) наиболее высокая, выявив тем самым структуру временного ряда. Если наиболее высоким оказывается значение r_t,t-1, то исследуемый ряд додержит только тенденцию. Если наиболее высоким оказался r_t,t-L, то ряд содержит (помимо тенденции) колебания периодом L. Если ни один из (l=1;L) не является значимым, можно сделать одно из двух предположений:

либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;
либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.

Последовательность коэффициентов автокорреляции 1, 2 и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости значений коэффициентов автокорреляции от величины лага (порядка коэффициента автокорреляции) называют коррелограммой.

Пример. В таблице приведены данные, отражающие спрос на некоторый товар за восьмилетний период (усл.ед.), то есть временный ряд спрос. Найти коэффициенты автокорреляции для лагов r=1,2 и частный коэффициент автокорреляции.

Год, t	1	2	3	4	5	6	7	8
Спрос, y	213	171	291	309	317	362	351	361

Решение. Сдвигаем исходный ряд на один уровень. Получаем следующую таблицу:

y_t	y_t-1
213	171
171	291
291	309
309	317
317	362
362	351
351	361

Расчет коэффициента автокорреляции первого порядка.
Параметры уравнения авторегрессии первого порядка.
Выборочные средние.

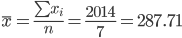
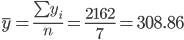
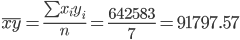
Выборочные дисперсии:

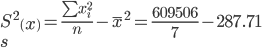
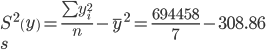
Среднеквадратическое отклонение

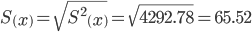
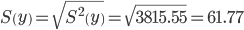
Коэффициент автокорреляции
Линейный коэффициент автокорреляции r_t,t-1:
r_t,t-2 =

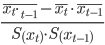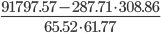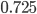
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < r_t,t-1< 0.3: слабая;
0.3 < r_t,t-1< 0.5: умеренная;
0.5 < r_t,t-1< 0.7: заметная;
0.7 < r_t,t-1< 0.9: высокая;
0.9 < r_t,t-1< 1: весьма высокая;
В нашем примере связь между рядами - высокая и прямая.

x	y	x²	y²	x • y
213	171	45369	29241	36423
171	291	29241	84681	49761
291	309	84681	95481	89919
309	317	95481	100489	97953
317	362	100489	131044	114754
362	351	131044	123201	127062
351	361	123201	130321	126711
2014	2162	609506	694458	642583

Частный коэффициент корреляции: Ф₁ = r₁
Сдвигаем исходный ряд на 2 уровней. Получаем следующую таблицу:

y_t	y_{t - 2}
213	291
171	309
291	317
309	362
317	351
362	361

Расчет коэффициента автокорреляции второго порядка.
Параметры уравнения авторегрессии второго порядка.
Выборочные средние.

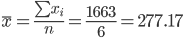
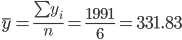
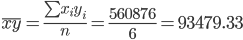
Выборочные дисперсии:

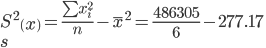
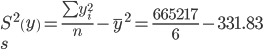
Среднеквадратическое отклонение

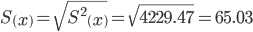
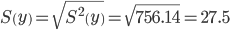
Коэффициент автокорреляции
Линейный коэффициент автокорреляции r_t,t-2:

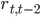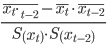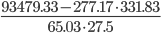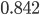
x	y	x²	y²	x • y
213	291	45369	84681	61983
171	309	29241	95481	52839
291	317	84681	100489	92247
309	362	95481	131044	111858
317	351	100489	123201	111267
362	361	131044	130321	130682
1663	1991	486305	665217	560876

Частный коэффициент корреляции:

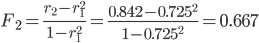
Лаг (порядок)	r_t,t-L	Коррелограмма
1	0.73	****
2	0.84	****

Вывод: в данном ряду динамики имеется тенденция (r_t,t-1 = 0.725 → 1). А также имеются периодические колебания с периодом, равным 2 (r_t,t-2=0.84 → 1).

Пример №2. 1. Рассчитать коэффициент автокорреляции 1-го порядка. Построить коррелограмму и сделать вывод о наличии сезонных колебаний.
2. Построить мультипликативную модель временного ряда. Сделать прогноз на следующие 2 дня.
3. Проверить гипотезу о наличии автокорреляции в остатках для модели данного временного ряда.

Пример №2. По данным, взятым из соответствующей таблицы, выполнить следующие действия:

Определить коэффициенты автокорреляции разного порядка и выбрать величину лага.
Построить авторегрессионную функцию. Определить экономический смысл ее параметров.
Рассчитать прогнозные значения на три года вперед.

Представлены сведения об уровне среднегодовых цен на говядину из США на рынках Нью-Йорка, амер. центы за фунт

Год	Цена	Год	Цена
1980	41	1994	97
1981	42	1995	89
1982	49	1996	77
1983	64	1997	81
1984	53	1998	82
1985	44	1999	87
1986	52	2000	94
1987	51	2001	90
1988	71	2002	90
1989	92	2003	93
1990	87	2004	87
1991	86	2005	84
1992	99	2006	85
1993	96	2007	86

Автокорреляция уровней временного ряда

Правила ввода данных

Поиск

Процесс

Сообщение