Коэффициент конкордации

Коэффициент конкордации является мерой согласованности мнений экспертов.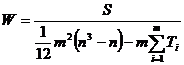

$Коэффициент конкордации$ ,

где

, L_i - число связок (видов повторяющихся элементов) в оценках i-го эксперта, t_l - количество элементов в l-й связке для i-го эксперта (количество повторяющихся элементов). Если нет связанных рангов, то T_i равно нулю.

Назначение сервиса. С помощью онлайн-калькулятора производится расчет коэффициента конкордации, а также делается вывод о его значимости.

Инструкция. Укажите Число факторов и Число экспертов. Полученное решение сохраняется в файле Word.

Скачать пример оформления

Пример. Шесть экспертов (n=6) ранжируют пять (m=5) элементов (X_1,X₂, …, X₃) по их важности. Результаты сведены в таблицу. Определить суммарную ранжировку этих элементов и коэффициент конкордации. Проверить значимость коэффициента конкордации, если табличное значение χ²_0,01(4) для 1% уровня значимости и 4 степеней (k = n-1=5-1=4) свободны равно 13,277.
Таблица - Расчет коэффициента конкордации

Эксперты ↓ Факторы→	1	2	3	4	5	6	r_j	d_i	d²
1	2	3	1	2	1	1	10	-8	64
2	1	1	3	3	4	2	14	-4	16
3	3	2	2	1	2	3	13	-5	25
4	4	5	4	5	3	4	25	7	49
5	5	4	5	4	5	5	28	10	100

Анализ строки r_j (суммы рангов, полученных элементом _X_jот всех экспертов) показывает, что наименьшее значение эта сумма имеет для первого элемента. Этому элементу приписывается ранг 1. Ранг 2 имеет 3-й элемент, ранг 3 имеет 2-й элемент, ранги 4 и 5 имеют 4-й и 5-й элементы соответственно.
Сумма рангов, проставленных всеми экспертами равна N·m·(m+1)/2 = 6·5·(5+1)/2=90. Если разделить это значение на количество ранжируемых элементов (6), получим среднее значение рангов, приходящихся на один элемент, равное 18. Вычтем это значение из суммы рангов, полученных элементом X_jот всех экспертов r_j (см. строку d_j табл.), возведем полученную разность в квадрат (см. строку d² табл.) и просуммируем для всех элементов. В результате получим величину R(d²)=254. Максимально возможное значение этой величины равно:

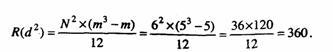
Коэффициент конкордации W=254/360=0,71.
Значение χ2 = N·(m-l)·W=6·(5-l)·0,71=17,04, т.к. χ²> χ²_0,01 (χ²_0,01(4) =13,27), следовательно, коэффициент значим, согласованность удовлетворительна.

Пример №2.
Цель решения задачи: использование полученной информации для определения путей качественного совершенствования продукции, оценки технического уровня, конкурентоспособности холодильников на рынке, обоснования цен, надбавок (скидок) с цен с учетом технического уровня продукции, выявления новых секторов рынка холодильников.
Задание. Произвести экспертную оценку технических параметров холодильников по степени значимости их для потребителей.

Исходные данные
Технические параметры холодильников:
1. Объем камеры м³.
2. Количество камер шт.
3. Энергопотребление.
4. Наличие системы Hoy Frost.
5. Дизайн.
6. Бренд.
Число факторов n= 6
Число экспертов m= 4

Решение
Видео решение

Решение находим с помощью калькулятора.
Этап 1. Создание экспертной комиссии.
В экспертную группу вошло 4 эксперта.

Этап 2. Сбор мнений специалистов путем анкетного опроса.
Оценку степени значимости технических параметров холодильника для потребителей эксперты производят путем присвоения им рангового номера. Фактору, которому эксперт дает наивысшую оценку, присваивается ранг 1. Если эксперт признает несколько факторов равнозначными, то им присваивается одинаковый ранговый номер. На основе данных анкетного опроса составляется сводная матрица рангов.

Этап 3. Составление сводной матрицы рангов.
Таблица 1
Матрица рангов

№ п/п	Технические параметры холодильника	Единица измерения	Эксперты
№ п/п	Технические параметры холодильника	Единица измерения	1	2	3	4
1	Объем камеры (x₁)	м³	3	4	5	4
2	Бренд (x₂)	-	5	6	3	4
3	Количество камер (x₃)	Шт.	4	3	1	3
4	Наличие систем Hoy Frost (x₄)	-	1	1	3	1
5	Энергопотребление (x₅)	Вт.	6	5	6	6
6	Дизайн (x₆)	-	2	2	2	2

Так как в матрице имеются связанные ранги (одинаковый ранговый номер) в оценках 3-его и 4-ого экспертов, произведем их переформирование. Переформирование рангов производиться без изменения мнения эксперта, то есть между ранговыми номерами должны сохраниться соответствующие соотношения (больше, меньше или равно). Также не рекомендуется ставить ранг выше 1 и ниже значения равного количеству параметров (в данном случае n= 6).
Переформирование рангов производится в табл. 2, 3
Таблица 2

Номера мест в упорядоченном ряду	1	2	3	4	5	6
Расположение факторов по оценке эксперта	1(x₃)	2(x₆)	3(x₂)	3(x₄)	5(x₁)	6(x₅)
Новые ранги	1	2	3,5	3,5	5	6

Таблица 3

Номера мест в упорядоченном ряду	1	2	3	4	5	6
Расположение факторов по оценке эксперта	1(x₄)	2(x₆)	3(x₃)	4(x₁)	4(x₂)	6(x₅)
Новые ранги	1	2	3	4,5	4,5	6

На основании переформирования рангов строится новая матрица рангов (табл. 4).
Матрица рангов
Таблица 4

Эксперты Факторы	1	2	3	4	Сумма рангов	Δ
x₁	3	4	5	4,5	16,5	2,5	6,25
x₂	5	6	3,5	4,5	19	5	25
x₃	4	3	1	3	11	-3	9
x₄	1	1	3,5	1	6,5	-7,5	56,25
x₅	6	5	6	6	23	9	81
x₆	2	2	2	2	8	-6	36
Σ	21	21	21	21	84	S = 213,5

.
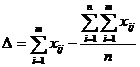Проверка правильности составления матрицы на основе исчисления контрольной суммы:

.
Сумма по столбцам матрицы равны между собой и контрольной суммы, значит матрица составлена правильно.

Этап 4. Анализ значимости исследуемых факторов.
В данном примере факторы по значимости распределились следующим образом (табл. 5).
Таблица 5 - Расположение факторов по значимости

Факторы	x₄	x₆	x₃	x₁	x₂	x₅
Сумма рангов	6,5	8	11	16,5	19	23

Для наглядности полученных результатов оценок факторов построим гистограмму и полигон распределения сумм рангов по степени их значимости для потребителей (рис. 1), проведем классификацию факторов по сумме рангов.

Рис. 1. Гистограмма и полигон распределения сумм рангов

Гистограмма (рис. 1) позволяет сделать следующие выводы:
1. Наибольшее значение для потребителей имеют фактор x₄ (наличие систем Hoy Frost) и фактор x₆ (дизайн).
2. Вторая группа по значимости включает в себя один фактор x₃ (количество камер).
3. Третья группа включает в себя факторы x₁ (объем камеры), x₂ (бренд), x₅ (энергопотребление).
Итак, важнейшими для потребителей являются следующие технические параметры холодильников: x₄, x₆, x₃.

Этап 5. Оценка средней степени согласованности мнений всех экспертов.
Воспользуемся коэффициентом конкордации для случая, когда имеются связанные ранги (одинаковые значения рангов в оценках одного эксперта)
,
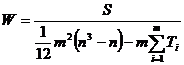где , L_i - число связок (видов повторяющихся элементов) в оценках i-го эксперта, t_l - количество элементов в l-й связке для i-го эксперта (количество повторяющихся элементов).
S = 213,5 (см. табл. 6.4), n = 6, m = 4,
(в оценках 3-его эксперта одна связка, повторяется ранг «3,5» 2 раза),
, (в оценках 4-ого эксперта одна связка, повторяется ранг «4,5» 2 раза),
, (если нет связанных рангов, то T_i равно нулю)
.
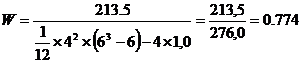W = 0.774 говорит о наличии высокой степени согласованности мнений экспертов. На высокую степень согласованности мнений экспертов указывает и полигон распределения сумм рангов (рис. 6.1). Ломанная и прямая линии близко расположены друг к другу.

Этап 6. Оценка значимости коэффициента конкордации.
Для этой цели исчислим критерий согласования Пирсона: , .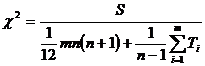
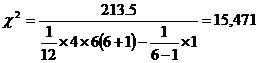Вычисленный сравним с табличным значением для числа степеней свободы K = n-1 = 6-1 = 5 и при заданном уровне значимости α = 0,05.
Так как расчетный 15,471 > табличного = 11,07, то W = 0.744 - величина не случайная, а потому полученные результаты по оценке качественных свойств холодильников по степени их значимости для потребителей имеют смысл и могут использоваться в дальнейших исследованиях.

Этап 7. Подготовка решения экспертной комиссии.
Была поставлена задача выяснить, какие технические параметры холодильников в наибольшей степени интересуют потребителей.
В результате проведенного исследования на основе экспертных оценок выяснилось, что важнейшими качественными свойствами являются: наличие систем, дизайн и количество камер. Следовательно, качественное совершенствование холодильников должны идти по пути улучшения этих свойств (исходя из требований НТП).
Себестоимость, цены, доплата к ценам на изделия улучшенного качества и скидки с цен на холодильники должны строиться с учетом вышеперечисленных качественных свойств.
На основе получения суммы рангов (табл. 4) можно вычислить показатели весомости рассмотренных технических параметров холодильников для потребителя с тем, чтобы их можно было учитывать при оценке технического уровня холодильников. Для этого произведем следующие вычисления. Сначала по каждому параметру вычислим величины, обратные сумме рангов, то есть
; ;
; ; .
Это делается для того, чтобы привести в соответствие содержание сумм рангов коэффициентам весомости. Расположим полученные числа по мере убывания, сложим их, взвесим каждое число в полученной сумме, которую примем равной 1 (табл. 6).