Выборочный метод в математической статистике
Выборочным методом называется метод решения этой задачи посредством анализа выборки, полученной в результате многократных наблюдений. Данный раздел представлен онлайн-калькуляторами:- Построение вариационных рядов. Пример. Дана выборка количества сделок, совершенных фирмой по работе с недвижимостью за 20 дней. Требуется:
а) составить таблицу, устанавливающую зависимость между значениями указанной случайной величины и ее частотами;
б) построить статистическое распределение и изобразить полигон распределения;
в) найти эмпирическую функцию распределения и изобразить ее график;
г) найти выборочное среднее, дисперсию, среднее квадратическое отклонение. - Построение доверительных интервалов для математического ожидания и среднего квадратического отклонения нормально распределенной случайной величины. Пример. Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 0.95, зная выборочную среднюю x, объем выборки n и среднее квадратическое отклонение σ.
- Проверка статистических гипотез
- Гипотеза о генеральном среднем значении нормального распределения при не известной дисперсии. В данном случае статистикой служит случайная величина
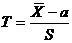, имеющая распределение Стьюдента. - Гипотеза о равенстве генеральных средних.
- Гипотеза о равенстве двух дисперсий.
- Гипотеза о генеральном среднем значении нормального распределения при не известной дисперсии. В данном случае статистикой служит случайная величина
- Показатели вариации
Выборочное наблюдение
Выборочное наблюдение имеет важное значение. Это связано с сокращением и упрощением отчетности в условиях рыночной экономики.Для вычисления средней ошибки выборки в том случае, когда генеральная совокупность представляется достаточно большой, или отношение численности выборки к численности генеральной совокупности (n:N) менее 5 %, то поправкой
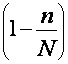можно пренебречь и находить ошибку выборки по способу повторного отбора, даже если сама выборка была бесповторной.
Наиболее частой ошибкой является отождествление средней ошибки, выборочной средней и средней ошибки выборочной доли. Изучая эту тему, надо хорошо усвоить, что средняя ошибка выборочной средней определяется по вариации количественного признака (x1,x2, …,xn):
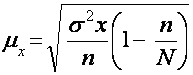(5) – (для поворотного, собственно случайного отбора).
Средняя ошибка выборочной доли
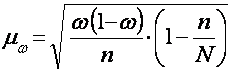(6) – (для поворотного случайного отбора) определяется по показателям дисперсии альтернативного признака [ω(1- ω)], где:
;
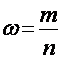m – численность единиц выборочной совокупности, обладающих исследуемым признаком.
В решении этих задач часто неверно указывается значение так называемого коэффициента доверия t при заданной степени вероятности. Значение t определяется по специальным таблицам, которые приведены в учебниках.
