Статистические гипотезы
На основе собранных в статистических исследованиях данных после их обработки делаются выводы об изучаемых явлениях. Эти выводы делаются путём выдвижения и проверки статистических гипотез.Типы ошибок. Выдвинутая гипотеза проверяется на основании исследования выборки, полученной из генеральной совокупности. Из-за случайности выборки в результате проверки не всегда делается правильный вывод. При этом могут возникать следующие ситуации:
1. Основная гипотеза верна и она принимается.
2. Основная гипотеза верна, но она отвергается.
3. Основная гипотеза не верна и она отвергается.
4. Основная гипотеза не верна, но она принимается.
Во случае 2 говорят об ошибке первого рода, в последнем случае речь идёт об ошибке второго рода.
Таким образом, по одним выборкам принимается правильное решение, а по другим – неправильное. Решение принимается по значению некоторой функции выборки, называемой статистической характеристикой, статистическим критерием или просто статистикой. Множество значений этой статистики можно разделить на два непересекающихся подмножества:
- подмножество значений статистики, при которых гипотеза Н0принимается (не отклоняется), называется областью принятия гипотезы (допустимой областью);
- подмножество значений статистики, при которых гипотеза Н0отвергается (отклоняется) и принимается гипотеза Н1,называется критической областью.
- Критерием называется случайная величина K, которая позволяет принять или отклонить нулевую гипотезу H0.
- При проверке гипотез можно допустить ошибки 2 родов.
Ошибка первого рода состоит в том, что будет отклонена гипотеза H0, если она верна ("пропуск цели"). Вероятность совершить ошибку первого рода обозначается α и называется уровнем значимости. Наиболее часто на практике принимают, что α = 0,05 или α = 0,01.
Ошибка второго рода заключается в том, что гипотеза H0 принимается, если она неверна ("ложное срабатывание"). Вероятность ошибки этого рода обозначается β.
Классификация гипотез
Основная гипотеза Н0 о значении неизвестного параметра q распределения обычно выглядит так:Н0: q = q0.
Конкурирующая гипотеза Н1 может при этом иметь следующий вид:
Н1: q < q0, Н1: q > q0 или Н1: q ≠ q0.
Соответственно получается левосторонняя, правосторонняя или двусторонняя критические области. Граничные точки критических областей (критические точки) определяют по таблицам распределения соответствующей статистики.
При проверке гипотезы разумно уменьшить вероятность принятия неправильных решений. Допустимая вероятность ошибки первого рода обозначается обычно a и называется уровнем значимости. Его значение, как правило, мало (0,1, 0,05, 0,01, 0,001…). Но уменьшение вероятности ошибки первого рода приводит к увеличению вероятности ошибки второго рода (b), т.е. стремление принимать только верные гипотезы вызывает возрастание числа отброшенных правильных гипотез. Поэтому выбор уровня значимости определяется важностью поставленной проблемы и тяжестью последствий неверно принятого решения.
Проверка статистической гипотезы состоит из следующих этапов:
1) определение гипотез Н0 и Н1;
2) выбор статистики и задание уровня значимости;
3) определение критических точек Ккр и критической области;
4) вычисление по выборке значения статистики Кэкс;
5) сравнение значения статистики с критической областью (Ккр и Кэкс);
6) принятие решения: если значение статистики не входит в критическую область, то принимается гипотеза Н0 и отвергается гипотеза H1, а если входит в критическую область, то отвергается гипотеза Н0 и принимается гипотеза Н1. При этом, результаты проверки статистической гипотезы нужно интерпретировать так: если приняли гипотезу Н1, то можно считать её доказанной, а если принялигипотезу Н0, то признали, что она не противоречит результатам наблюдений.Однако этим свойством наряду с Н0 могут обладать и другие гипотезы.
Классификация проверок гипотез
Рассмотрим далее несколько различных статистических гипотез и механизмов их проверки.I. Гипотеза о генеральном среднем значении нормального распределения при не известной дисперсии
Предполагаем, что генеральная совокупность имеет нормальное распределение, её среднее и дисперсия неизвестны, но есть основания полагать, что генеральное среднее равно a. При уровне значимости α нужно проверить гипотезу Н0: x=a. В качестве альтернативной можно использовать одну из трёх рассмотренных выше гипотез. В данном случае статистикой служит случайная величина
, имеющая распределение Стьюдента с n – 1 степенями свободы. Определяется соответствующее экспериментальное (наблюдаемое) значение tэкс. Из таблицы критических точек распределения Стьюдента находится критическое значение tкр. При альтернативной гипотезе Н1: x>a оно находится по уровню значимости α и числу степеней свободы n – 1. Если tэкс < tкр, то нулевая гипотеза принимается, в противоположном случае – отвергается. При альтернативной гипотезе Н1: x≠a критическое значение находится по уровню значимости α/2 и том же числе степеней свободы. Нулевая гипотеза принимается, если |tэкс|<tкр.
II) Гипотеза о равенстве двух средних значений произвольно распределённых генеральных совокупностей (большие независимые выборки). При уровне значимости α нужно проверить гипотезу Н0: x≠y. Если объём обеих выборок велик, то можно считать, что выборочные средние имеют нормальное распределение, а их дисперсии известны. В этом случае в качестве статистики можно использовать случайную величину
,
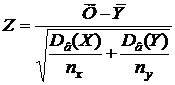имеющую нормальное распределение, причём M(Z) = 0, D(Z) = 1. Определяется соответствующее экспериментальное значение zэкс. Из таблицы функции Лапласа находится критическое значение zкр. При альтернативной гипотезе Н1: x>y оно находится из условия F(zкр) = 0,5 – a. Если zэкс < zкр, то нулевая гипотеза принимается, в противоположном случае – отвергается. При альтернативной гипотезе Н1: x≠y критическое значение находится из условия F(zкр) = 0,5×(1 – a). Нулевая гипотеза принимается, если |zэкс| < zкр.
III) Гипотеза о равенстве двух средних значений нормально распределённых генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки). При уровне значимости α нужно проверить основную гипотезу Н0: x=y. В качестве статистики используем случайную величину
,
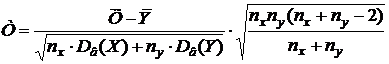имеющую распределение Стьюдента с (nх + nу – 2) степенями свободы. Определяется соответствующее экспериментальное значение tэкс. Из таблицы критических точек распределения Стьюдента находится критическое значение tкр. Всё решается аналогично гипотезе (I).
IV) Гипотеза о равенстве двух дисперсий нормально распределённых генеральных совокупностей. В данном случае при уровне значимостиaнужно проверить гипотезу Н0: D(Х) = D(Y). Статистикой служит случайная величина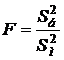 
, имеющая распределение Фишера – Снедекора с f1 = nб – 1 и f2 = nм – 1 степенями свободы (S2б – большая дисперсия, объём её выборки nб). Определяется соответствующее экспериментальное (наблюдаемое) значение Fэкс. Критическое значение Fкр при альтернативной гипотезе Н1: D(Х) > D(Y) находится из таблицы критических точек распределения Фишера – Снедекора по уровню значимости a и числу степеней свободы f1 и f2. Нулевая гипотеза принимается, если Fэкс < Fкр.
V) Гипотеза о равенстве нескольких дисперсий нормально распределённых генеральных совокупностей по выборкам одинакового объёма. В данном случае при уровне значимостиaнужно проверить гипотезу Н0: D(Х1) = D(Х2) = …= D(Хl). Статистикой служит случайная величина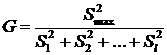 
, имеющая распределение Кочрена со степенями свободыf = n – 1 и l (n – объём каждой выборки, l – количество выборок). Проверка этой гипотезы проводится так же, как и предыдущей. Используется таблица критических точек распределения Кочрена.
VI) Гипотеза о существенности корреляционной связи. В данном случае при уровне значимостиaнужно проверить гипотезу Н0: r = 0. (Если коэффициент корреляции равен нулю, то соответствующие величины не связаны друг с другом). Статистикой в данном случае служит случайная величина
,
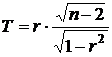имеющая распределение Стьюдента с f = n – 2 числом степеней свободы. Проверка этой гипотезы проводится аналогично проверке гипотезы (I).
VII) Гипотеза о значении вероятности появления события. Проведено достаточно большое количество n независимых испытаний, в которых событие А произошло m раз. Есть основания полагать, что вероятность наступления данного события в одном испытании равна р0. Требуется при уровне значимостиaпроверить гипотезу о том, что вероятность события А равна гипотетической вероятности р0. (Т.к. вероятность оценивается по относительной частоте, то проверяемую гипотезу можно сформулировать и иначе: значимо или нет различаются наблюдаемая относительная частота и гипотетическая вероятность).
Количество испытаний достаточно велико, поэтому относительная частота события А распределена по нормальному закону. Если нулевая гипотеза верна, то её математическое ожидание равно р0, а дисперсия 
. В соответствии с этим в качестве статистики выберем случайную величину
,
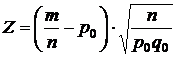которая распределена приближённо по нормальному закону с нулевым математическим ожиданием и единичной дисперсией. Проверка данной гипотезы осуществляется точно так же, как и в случае (I).
VIII) Гипотеза о виде распределения генеральной совокупности. Критерий согласия Пирсона. На основании выборки из генеральной совокупности или из каких-то иных соображений выдвигается нулевая гипотеза о конкретном распределении генеральной совокупности, выраженной через функцию распределения F(x). Это распределение назовём теоретическим.
По выборке находится эмпирическая функция распределения F*(x). Гипотеза Н0 о распределении генеральной совокупности принимается, если эмпирическое распределение хорошо согласуется с теоретическим. Для проверки таких гипотез разработаны несколько критериев согласия. Здесь рассматривается c2-критерий согласия Пирсона.
При его использовании вся область изменения генеральной совокупности делится на несколько интервалов, которые могут иметь различную длину. По выборке составляют вариационный ряд с использованием этих же интервалов. Если в некотором интервале частота, слишком мала (меньше 4), то этот интервал объединяют с соседним.
По выборке вычисляют оценки параметров теоретического распределения. Тем самым теоретическое распределение будет полностью определено. Далее по теоретическому распределению находятся вероятности того, что случайная величина принимает значение из каждого интервала. После чего вычисляются теоретические частоты (произведения найденной вероятности на объём выборки).
Нулевая гипотеза принимается, если теоретические и эмпирические частоты мало отличаются друг от друга. При этом в качестве статистики рассматривается случайная величина
,
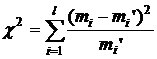где mi – эмпирические, а mi’ – теоретические частоты, l – количество интервалов. Эта величина имеет распределение c2 с l – p – 1 степенями свободы (где р – число подбираемых параметров распределения). Основная гипотеза о виде распределения принимается, если χнабл<χкр.
Калькулятор о виде распределения
Дисперсионный анализ
Тесно связан с задачами статистической проверки статистических гипотез дисперсионный анализ, в котором проверяется гипотеза о равенстве нескольких генеральных средних Н0: М(Х1) = М(Х2) = … М(Хl). При этом предполагаемое различие генеральных средних обусловлено действием некоторого фактора. А рассматриваемые генеральные совокупности (группы) отличаются значением данного действующего фактора (эти значения называют в дисперсионном анализе уровнями или градациями и они могут быть как количественными, так и качественными). Поэтому, подтверждение в результате проверки различия генеральных средних будет одновременно и доказательством действия данного фактора.Различия вариант в группах обуславливаются как естественным разбросом данной величины, так и действием исследуемого фактора. Поэтому в рассмотрение вводятся две дисперсии: остаточная или внутригрупповая (она отражает естественный разброс вариант) и факторная или межгрупповая (характеризует разброс, вызванный действием фактора). Эти дисперсии сравниваются по критерию Фишера. Их различие означает и различие генеральных средних, а поэтому и действие фактора. И наоборот.
В дисперсионном анализе предполагается равенство групповых дисперсий. Поэтому перед его проведением желательно проверить их равенство; например, по критерию Кочрена или Бартлетта.
Факторная и остаточная дисперсии находятся по формулам
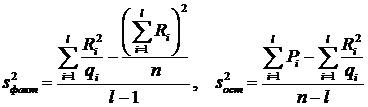, (15)
где
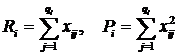. В этих формулах n – общее количество всех вариант, l – число уровней фактора, qi – количество вариант на i-том уровне, xij – значение варианты, x – общее среднее, xi – среднее на i-том уровне. Легко видеть, что при отсутствии влияния фактора обе эти дисперсии являются несмещёнными оценками генеральной дисперсии. При проверке критерия Фишера число степеней свободы f1 = l – 1, f2 = n – l.
Кроме рассмотренного сейчас однофакторного дисперсионного анализа часто применяется и многофакторный анализ. При этом исследуется влияние на изучаемый признак сразу нескольких внешних причин. В отличие от однофакторного анализа в многофакторном применяются только равномерные выборки. Причём, обычно используются полные планы (должны быть задействованы все комбинации уровней факторов).
Для двухфакторного дисперсионного анализа факторные и остаточная дисперсии находятся по формулам:
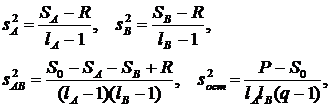(16)
где s2A, s2B, s2AB – дисперсии факторов A, B и их комбинации (взаимодействия), lA, lB – число уровней факторов A и B, а остальные величины находятся по следующим формулам:
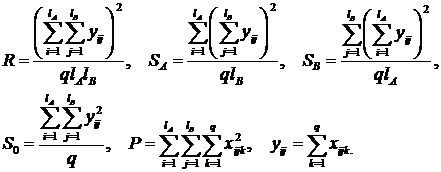(17)
Число степеней свободы для фактора А fA = lA – 1, фактора В fB = lB – 1, их совместного влияния fAB = (lA – 1)(lB – 1), f2 = lAlB(q – 1).
