Аналитическая группировка
Аналитическая группировка – группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками.Назначение сервиса. С помощью сервиса в онлайн режиме производится аналитическая группировка ряда (метод статистических группировок), по которой проводится дисперсионный анализ - вычисляются: общая дисперсия, межгрупповая и средняя из групповых дисперсий, а также коэффициент детерминации (см. пример). Результаты аналитической группировки также можно использовать для построения типологической группировки или комбинированной группировки или уравнения регрессии.
Пример №1. По ряду предприятий получены данные, указанные в таблице (Среднесписочное число рабочих, чел.; основные средства, тыс. руб.; объем произведенной продукции за год, млн. руб.):
- Постройте ряд распределения предприятий по числу рабочих, образовав, пять групп с равными интервалами;
- Охарактеризуйте ряд числом рабочих, объемом произведенной продукции за год, объемом основных средств;
- Рассчитайте по полученным данным среднюю, модальную и медианную численность работников предприятий отрасли, показатели вариации.
- скопировать два столбца: Среднесписочное число рабочих и Объем произведенной продукции (по каждой группе будет рассчитан объем произведенной продукции - столбец Y);
- скопировать два столбца: Среднесписочное число рабочих и Основные средства(по каждой группе будет рассчитан объем основных средств - столбец Y).
Алгоритм метода аналитической группировки
Всю совокупность признаков можно разделить на две группы: факторные и результативные. Факторными называются признаки, под воздействием которых меняются, другие результативные, признаки. Взаимосвязь проявляется в том, что с возрастанием значения факторного признака возрастает или убывает среднее значение результативного.- Упорядочить совокупность данных по X.
- Найти ширину интервала h = (Xmax - Xmin)/n, где n - количество групп
- Образовать интервальный ряд, подсчитывая в каждую группу сумму значений Y.
Особенности аналитической группировки:
- в основу группировки кладется факторный признак;
- каждая выделенная группа характеризуется средними значениями результативного признака.
Пример №2. По данным таблицы 2 :
1) произвести группировку 40 коммерческих банков РФ по величине:
а) кредитных вложений;
б) объём вложений в ценные бумаги.
К каждой выделенной группе подберите 3-4 наиболее экономически связанных и существенных показателя, имеющихся в таблице, а также вычислите показатели в относительном выражении. Результаты группировки изложите в свободных таблицах и проанализируйте;
2) с помощью аналитической группировки проанализируйте зависимость величины прибыли от других экономических показателей, характеризующих деятельность 40 коммерческих банков. Результаты оформите в таблице. Сделайте выводы;
3) проведите комбинационную группировку 40 коммерческих банков по двум признакам: величине кредитных вложений и объему вложений в ценные бумаги.
Проанализируйте полученную группировку. Сделайте выводы.
Решение:
Описание параметров
Количество строк: количество исходных данных. Если размерность ряда небольшая, укажите его количество. Если выборка достаточно объемная, то нажмите кнопку Вставить из Excel. Скопируйте из Excel два столбца (первый столбец - первичный признак для группировки, второй столбец - вторичный).
Количество групп: 0 – число групп будет определяться по формуле Стэрджесса.
Если задано конкретное число групп, укажите его (например, 5).
Проанализируем зависимость величины прибыли от объёма вложений в ценные бумаги. Вставляем из Excel следующие данные: первый столбец - значения прибыли, второй столбец – значения объёма вложений в ценные бумаги.
Пример №3. Имеются данные о заработной плате рабочих бригады за месяц.
| Табельный номер рабочего | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Процент выполнения норм выработки | 110,8 | 102,0 | 111,0 | 107,8 | 106,4 | 109,0 | 100,0 | 105,0 |
| Заработная плата за месяц, руб. | 11730 | 10800 | 12300 | 14400 | 11550 | 11940 | 10200 | 11100 |
На основе выполненной группировки построить групповую таблицу.
Сформулировать выводы.
Метод статистических группировок в изучении производственных показателей
Задание №1: Имеются следующие данные по группе промышленных предприятий за отчетный год:Таблица №1
| № предприятия | Среднегодовая стоимость основных средств, млрд. руб | Прибыль, млн. руб. |
| 1 | 10 | 13,5 |
| 2 | 22,8 | 136,2 |
| 3 | 18,4 | 97,6 |
| 4 | 12,6 | 44,4 |
| 5 | 22 | 146 |
| 6 | 19 | 110,4 |
| 7 | 21,6 | 138,7 |
| 8 | 9,4 | 30,6 |
| 9 | 19,4 | 111,8 |
| 10 | 13,6 | 49,6 |
| 11 | 17,6 | 105,8 |
| 12 | 8,8 | 30,7 |
| 13 | 14 | 64,8 |
| 14 | 10,2 | 33,3 |
Решение:
1. Для решения подобных задач служит сервис «Аналитическая группировка». Первым шагом необходимо будет ввести исходные данные. Возможны два способа ввода: вручную и вставкой из Excel. Если данных очень много, рекомендуем воспользоваться вторым способом. В данном примере используем именно этот способ, поэтому поле «Количество строк» не заполняем.
2. Поскольку в задании имеется требование о применении формулы Стерджесса, то поле «Количество групп» оставляем без изменений (значение 0).
3. Нажимаем кнопку «Вставить из Excel». Появится страница следующего вида (рис. 1):

Рисунок 1 – Ввод исходных данных через Excel
4. Вставляем наши данные в поле для ввода.

Рисунок 2 – Вставка данных из Excel
5. Нажимаем кнопку «Далее», получаем заполненные исходные данные для обработки:
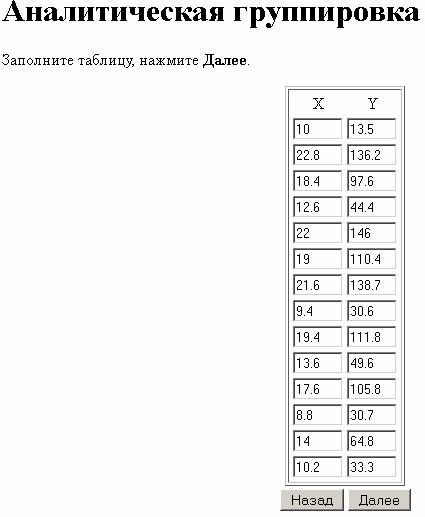
Рисунок 3 – Заполненные исходные данные для обработки
6. Получаем решение в формате Word (скачать).
Группировка строится на основе следующей таблицы.
Таблица №2
| 8.8 | 8.8 - 11.8 | 1 |
| 9.4 | 8.8 - 11.8 | 2 |
| 10 | 8.8 - 11.8 | 3 |
| 10.2 | 8.8 - 11.8 | 4 |
| 12.6 | 11.8 - 14.8 | 1 |
| 13.6 | 11.8 - 14.8 | 2 |
| 14 | 11.8 - 14.8 | 3 |
| 17.6 | 14.8 - 17.8 | 1 |
| 18.4 | 17.8 - 20.8 | 1 |
| 19 | 17.8 - 20.8 | 2 |
| 19.4 | 17.8 - 20.8 | 3 |
| 21.6 | 20.8 - 23.8 | 1 |
| 22 | 20.8 - 23.8 | 2 |
| 22.8 | 20.8 - 23.8 | 3 |
Например, значения 8.8, 9.4, 10, 10.2 входят в группу [8.8 - 11.8] и их общее количество равно четырем. Сумма их равна 38.4 (8.8+9.4+10+10.2). Для этой же группы суммарная прибыль составит 108.1 млн. руб.(30.7+30.6+33.3+13.5).
Дадим интерпретацию полученным результатам.
Таблица №3
| Группы | ∑X | Кол-во, n | Xcp = ∑X / n | ∑Y | Ycp = ∑Y / n |
| 8.8 - 11.8 | 38.4 | 4 | 9.6 | 108.1 | 27.03 |
| 11.8 - 14.8 | 40.2 | 3 | 13.4 | 158.8 | 52.93 |
| 14.8 - 17.8 | 17.6 | 1 | 17.6 | 105.8 | 105.8 |
| 17.8 - 20.8 | 56.8 | 3 | 18.93 | 319.8 | 106.6 |
| 20.8 - 23.8 | 66.4 | 3 | 420.9 | 140.3 | 42.93 |
|
| 14 | 1113.4 |
Здесь ∑X – сумма среднегодовой стоимости основных средств, значения которых лежат в заданных пределах, млрд. руб.;
n – количество предприятий в каждой группе;
∑Y – сумма прибыли, значения которых лежат в заданных пределах, млн. руб.
7. Какие показатели можно рассчитать на основе полученных данных? Обычно это отношение столбцов 4 и 6. Например, если разделить значения столбца 4 на значения столбца 6, то получим, сколько основных фондов (руб.) приходится на 1 рубль прибыли.
Кроме этого, можно сказать о предварительной взаимосвязи анализируемых показателей, нанеся средние значения Хср и Ycp на график.
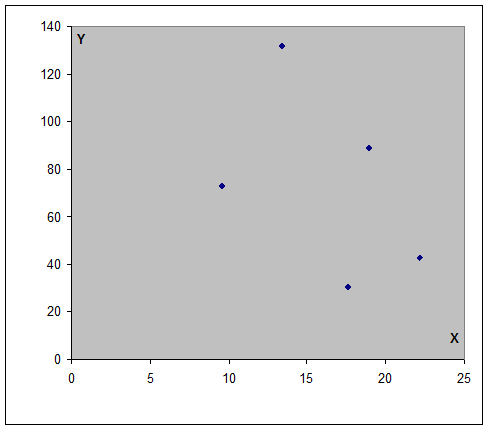
Рисунок 4 – График для X, Y (определение связи)
Судя по графику, можно судить о прямой зависимости, т.е. чем больше Х (стоимость основных фондов), тем больше Y (средняя прибыль на группу).
Примечание:
Иногда в задачах требуется сгруппировать данные из трех столбцов. Пусть имеется следующая таблица.
| № предприятия | Среднегодовая стоимость основных средств, млрд. руб | Прибыль, млн. руб. | Валовая продукция,
млн. руб. |
| 1 | 10 | 13,5 | 13,5 |
| 2 | 22,8 | 136,2 | 136,2 |
| 3 | 18,4 | 97,6 | 97,6 |
| 4 | 12,6 | 44,4 | 44,4 |
| 5 | 22 | 146 | 146 |
| 6 | 19 | 110,4 | 110,4 |
| 7 | 21,6 | 138,7 | 138,7 |
| 8 | 9,4 | 30,6 | 30,6 |
| 9 | 19,4 | 111,8 | 111,8 |
| 10 | 13,6 | 49,6 | 49,6 |
| 11 | 17,6 | 105,8 | 105,8 |
| 12 | 8,8 | 30,7 | 30,7 |
| 13 | 14 | 64,8 | 64,8 |
| 14 | 10,2 | 33,3 | 33,3 |
а) получаем решение для столбцов «Среднегодовая стоимость основных средств» и «Прибыль»;
б) получаем решение для столбцов «Среднегодовая стоимость основных средств» и «Валовая продукция»;
в) объединяем решения.
Задание №2. Имеются отчетные данные 22 заводов одной из отраслей промышленности, приведенные в приложении А. С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов (Ф) и выпуском валовой продукции (ВП) произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав, пять групп заводов с равными интервалами. По каждой группе и совокупности подсчитайте:
а) число заводов, построив для этого табл. 1.2;
б) среднегодовую стоимость основных производственных фондов, всего и в среднем на один завод;
в) стоимость валовой продукции на один рубль основных производственных фондов (фондоотдачу).
Решение.
1. Нажимаем кнопку Вставить из Excel. Копируем два столба (первый столбец - среднегодовая стоимость основных производственных фондов, второй столбец - выпуск валовой продукции) в поле ввода.
2. Число заводов будет подсчитано в третьем столбце таблицы (см. таблицу №3).
3. Среднегодовая стоимость основных производственных фондов (всего) - во втором столбце (∑X); в среднем на один завод - в четвертом столбце (∑X/n).
4. Стоимость валовой продукции на один рубль основных производственных фондов (фондоотдача) - необходимо будет найти отношение четвертого столбца к шестому ([Xср]/[Yср]).
Задание №3. За отчетный период имеются следующие данные об электровооруженности труда и выработке продукции рабочими завода: Электровооруженность труда одного рабочего, кВт/ч; Выработка продукции на одного рабочего, млн. руб.
Для изучения зависимости между электровооруженностью труда и выработкой продукции сгруппируйте рабочих по электровооруженности труда, образовав четыре группы с равными интервалами. По каждой группе и в целом по совокупности рабочих подсчитайте:
1) число рабочих;
2) среднюю электровооруженность труда рабочих;
3) среднюю выработку продукции на одного рабочего.
Результаты представьте в таблице. Дайте анализ показателей и сделайте выводы.
Решение.
Указываем Количество групп: 4. Нажимаем кнопку Вставить из Excel.
В отчете в таблице будут указаны:
1) число рабочих (столбец №3, n);
2) средняя электровооруженность труда рабочих (столбец №4, Xср);
3) средняя выработка продукции на одного рабочего(столбец №6, Yср).
Пример №2. Имеются следующие выборочные данные за отчетный период по предприятиям одной из корпораций (выборка 10%-ная, механическая):
| № предприятия | Среднесписочная численность работников, чел. | Объем выпуска продукции, млн руб. | № предприятия | Среднесписочная численность работников, чел | Объем выпуска продукции, млн руб. |
| 1 | 221 | 426,45 | 16 | 232 | 466,94 |
| 2 | 156 | 391,95 | 17 | 108 | 273,33 |
| 3 | 225 | 436,54 | 18 | 264 | 561,22 |
| 4 | 251 | 499,75 | 19 | 122 | 315,67 |
| 5 | 265 | 581,42 | 20 | 150 | 358,20 |
| 6 | 158 | 356,20 | 21 | 199 | 381,80 |
| 7 | 120 | 269,20 | 22 | 242 | 459,20 |
| 8 | 190 | 444,72 | 23 | 293 | 597,13 |
| 9 | 253 | 430,42 | 24 | 178 | 368,44 |
| 10 | 179 | 360,21 | 25 | 227 | 483,34 |
| 11 | 267 | 512,42 | 26 | 308 | 716,20 |
| 12 | 304 | 654,32 | 27 | 266 | 551,83 |
| 13 | 191 | 461,61 | 28 | 307 | 689,35 |
| 14 | 201 | 395,82 | 29 | 211 | 475,90 |
| 15 | 110 | 256,20 | 30 | 189 | 450,22 |
Задание 2
По исходным данным с использованием результатов выполнения задания 1:
1) установите наличие и характер корреляционной связи между признаками «среднесписочная численность работников» и «объем выпуска продукции», используя метод аналитической группировки;
2) оцените силу и тесноту корреляционной связи между названными признаками, используя коэффициент детерминации, эмпирическое корреляционное отношение;
3) оцените статистическую значимость показателя силы связи. Сделайте выводы по результатам выполнения задания.
Решение. Задачу выполняем с помощью калькулятора метод аналитической группировки
.
Ширина интервала составит: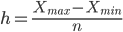
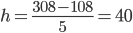
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
| 108 | 108 - 148 | 1 |
| 110 | 108 - 148 | 2 |
| 120 | 108 - 148 | 3 |
| 122 | 108 - 148 | 4 |
| 150 | 148 - 188 | 1 |
| 156 | 148 - 188 | 2 |
| 158 | 148 - 188 | 3 |
| 178 | 148 - 188 | 4 |
| 179 | 148 - 188 | 5 |
| 189 | 188 - 228 | 1 |
| 190 | 188 - 228 | 2 |
| 191 | 188 - 228 | 3 |
| 199 | 188 - 228 | 4 |
| 201 | 188 - 228 | 5 |
| 211 | 188 - 228 | 6 |
| 221 | 188 - 228 | 7 |
| 225 | 188 - 228 | 8 |
| 227 | 188 - 228 | 9 |
| 232 | 228 - 268 | 1 |
| 242 | 228 - 268 | 2 |
| 251 | 228 - 268 | 3 |
| 253 | 228 - 268 | 4 |
| 264 | 228 - 268 | 5 |
| 265 | 228 - 268 | 6 |
| 266 | 228 - 268 | 7 |
| 267 | 228 - 268 | 8 |
| 293 | 268 - 308 | 1 |
| 304 | 268 - 308 | 2 |
| 307 | 268 - 308 | 3 |
| 308 | 268 - 308 | 4 |
| Группы | № | Кол-во, nj | ∑X | Xcp = ∑Xj / nj | ∑Y | Ycp = ∑Yj / nj |
| 108 - 148 | 1,2,3,4 | 4 | 460 | 115 | 1114.4 | 278.6 |
| 148 - 188 | 5,6,7,8,9 | 5 | 821 | 164.2 | 1835 | 367 |
| 188 - 228 | 10,11,12,13,14,15,16,17,18 | 9 | 1854 | 206 | 3956.4 | 439.6 |
| 228 - 268 | 19,20,21,22,23,24,25,26 | 8 | 2040 | 255 | 4063.2 | 507.9 |
| 268 - 308 | 27,28,29,30 | 4 | 1212 | 303 | 2657 | 664.25 |
| Итого | 30 | 6387 | 13626 |
1. Находим средние значения каждой группы.
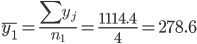
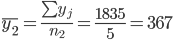
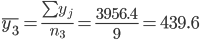
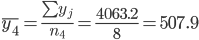
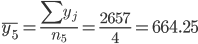
Общее средние значение для всей совокупности:
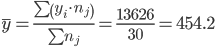
2. Дисперсия внутри группы при относительном постоянстве признака-фактора возникает за счет других факторов (не связанных с изучением). Эта дисперсия называется остаточной:
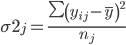
Расчет для группы: 108 - 148 (1,2,3,4)
| yj | (yj - yср)2 | Результат |
| 273.33 | (273.33 - 278.6)2 | 27.77 |
| 256.2 | (256.20 - 278.6)2 | 501.76 |
| 269.2 | (269.20 - 278.6)2 | 88.36 |
| 315.67 | (315.67 - 278.6)2 | 1374.18 |
| Итого | 1992.08 |
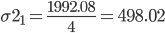
Расчет для группы: 148 - 188 (5,6,7,8,9)
| yj | (yj - yср)2 | Результат |
| 358.2 | (358.20 - 367)2 | 77.44 |
| 391.95 | (391.95 - 367)2 | 622.5 |
| 356.2 | (356.20 - 367)2 | 116.64 |
| 368.44 | (368.44 - 367)2 | 2.07 |
| 360.21 | (360.21 - 367)2 | 46.1 |
| Итого | 864.76 |
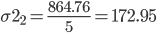
Расчет для группы: 188 - 228 (10,11,12,13,14,15,16,17,18)
| yj | (yj - yср)2 | Результат |
| 450.22 | (450.22 - 439.6)2 | 112.78 |
| 444.72 | (444.72 - 439.6)2 | 26.21 |
| 461.61 | (461.61 - 439.6)2 | 484.44 |
| 381.8 | (381.80 - 439.6)2 | 3340.84 |
| 395.82 | (395.82 - 439.6)2 | 1916.69 |
| 475.9 | (475.90 - 439.6)2 | 1317.69 |
| 426.45 | (426.45 - 439.6)2 | 172.92 |
| 436.54 | (436.54 - 439.6)2 | 9.36 |
| 483.34 | (483.34 - 439.6)2 | 1913.19 |
| Итого | 9294.13 |
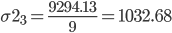
Расчет для группы: 228 - 268 (19,20,21,22,23,24,25,26)
| yj | (yj - yср)2 | Результат |
| 466.94 | (466.94 - 507.9)2 | 1677.72 |
| 459.2 | (459.20 - 507.9)2 | 2371.69 |
| 499.75 | (499.75 - 507.9)2 | 66.42 |
| 430.42 | (430.42 - 507.9)2 | 6003.15 |
| 561.22 | (561.22 - 507.9)2 | 2843.02 |
| 581.42 | (581.42 - 507.9)2 | 5405.19 |
| 551.83 | (551.83 - 507.9)2 | 1929.84 |
| 512.42 | (512.42 - 507.9)2 | 20.43 |
| Итого | 20317.47 |
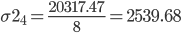
Расчет для группы: 268 - 308 (27,28,29,30)
| yj | (yj - yср)2 | Результат |
| 597.13 | (597.13 - 664.25)2 | 4505.09 |
| 654.32 | (654.32 - 664.25)2 | 98.6 |
| 689.35 | (689.35 - 664.25)2 | 630.01 |
| 716.2 | (716.20 - 664.25)2 | 2698.8 |
| Итого | 7932.51 |
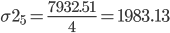
3. Внутригрупповые дисперсии объединяются в средней величине внутригрупповых дисперсий:
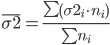
Средняя из частных дисперсий:
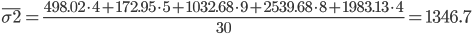
4. Межгрупповая дисперсия относится на счет изучаемого фактора, она называется факторной
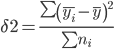
δ2 = ((278.6-454.2)2*4 + (367-454.2)2*5 + (439.6-454.2)2*9 + (507.9-454.2)2*8 + (664.25-454.2)2*4)/30 = 12094.42
Определяем общую дисперсию по всей совокупности, используя правило сложения дисперсий:
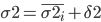
σ2 = 1346.7 + 12094.42 = 13441.12
Проверим этот вывод путем расчета общей дисперсии обычным способом:
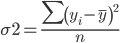
| yi | (yi - yср)2 | Результат |
| 273.33 | (273.33 - 454.2)2 | 32713.96 |
| 256.2 | (256.20 - 454.2)2 | 39204 |
| 269.2 | (269.20 - 454.2)2 | 34225 |
| 315.67 | (315.67 - 454.2)2 | 19190.56 |
| 358.2 | (358.20 - 454.2)2 | 9216 |
| 391.95 | (391.95 - 454.2)2 | 3875.06 |
| 356.2 | (356.20 - 454.2)2 | 9604 |
| 368.44 | (368.44 - 454.2)2 | 7354.78 |
| 360.21 | (360.21 - 454.2)2 | 8834.12 |
| 450.22 | (450.22 - 454.2)2 | 15.84 |
| 444.72 | (444.72 - 454.2)2 | 89.87 |
| 461.61 | (461.61 - 454.2)2 | 54.91 |
| 381.8 | (381.80 - 454.2)2 | 5241.76 |
| 395.82 | (395.82 - 454.2)2 | 3408.22 |
| 475.9 | (475.90 - 454.2)2 | 470.89 |
| 426.45 | (426.45 - 454.2)2 | 770.06 |
| 436.54 | (436.54 - 454.2)2 | 311.88 |
| 483.34 | (483.34 - 454.2)2 | 849.14 |
| 466.94 | (466.94 - 454.2)2 | 162.31 |
| 459.2 | (459.20 - 454.2)2 | 25 |
| 499.75 | (499.75 - 454.2)2 | 2074.8 |
| 430.42 | (430.42 - 454.2)2 | 565.49 |
| 561.22 | (561.22 - 454.2)2 | 11453.28 |
| 581.42 | (581.42 - 454.2)2 | 16184.93 |
| 551.83 | (551.83 - 454.2)2 | 9531.62 |
| 512.42 | (512.42 - 454.2)2 | 3389.57 |
| 597.13 | (597.13 - 454.2)2 | 20428.98 |
| 654.32 | (654.32 - 454.2)2 | 40048.01 |
| 689.35 | (689.35 - 454.2)2 | 55295.52 |
| 716.2 | (716.20 - 454.2)2 | 68644 |
| Итого | 403233.56 |
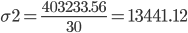
Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Это отношение факторной дисперсии к общей дисперсии:
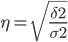
Определяем эмпирическое корреляционное отношение:

Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < η < 0.3: слабая;
0.3 < η < 0.5: умеренная;
0.5 < η < 0.7: заметная;
0.7 < η < 0.9: высокая;
0.9 < η < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X весьма высокая
Коэффициент детерминации.
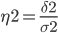
Определим коэффициент детерминации:
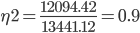
Таким образом, на 89.98% вариация обусловлена различиями между признаками, а на 10.02% – другими факторами.
Пример. По данным приложения 1 с целью изучения зависимости между факторным и результативным признаками произведите аналитическую группировку с равными интервалами.
По каждой группе и по совокупности предприятий подсчитайте:
- число предприятий;
- удельный вес предприятий группы (в % к итогу);
- размер факторного признака - всего по группе и в среднем на одно предприятие;
- размер результативного признака - всего по группе и в среднем на одно предприятие.



