Проверка гипотезы о равномерном распределении
В качестве примера непрерывной случайной величины рассмотрим случайную величину X, равномерно распределенную на интервале (a; b). Говорят, что случайная величина X равномерно распределена на промежутке (a; b), если ее плотность распределения непостоянна на этом промежутке:
Из условия нормировки определим значение константы c. Площадь под кривой плотности распределения должна быть равна единице, но в нашем случае — это площадь прямоугольника с основанием (b - α) и высотой c (рис. 1).
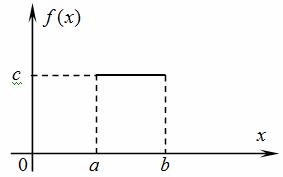
Рис. 1 Плотность равномерного распределения
Отсюда находим значение постоянной c:
Итак, плотность равномерно распределенной случайной величины равна
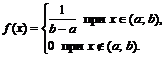
Найдем теперь функцию распределения по формуле:
1) для
2) для
3) для
0+1+0=1.
Таким образом,
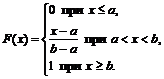
Функция распределения непрерывна и не убывает (рис. 2).
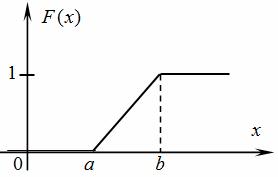
Рис. 2 Функция распределения равномерно распределенной случайной величины
Найдем математическое ожидание равномерно распределенной случайной величины по формуле:
Дисперсия равномерного распределения рассчитывается по формуле и равна 
Пример №1. Цена деления шкалы измерительного прибора равна 0.2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка: а) меньшая 0.04; б) большая 0.02
Решение. Ошибка округления есть случайная величина, равномерно распределенная на промежутке между соседними целыми делениями. Рассмотрим в качестве такого деления интервал (0; 0,2) (рис. а). Округление может проводиться как в сторону левой границы — 0, так и в сторону правой — 0,2, значит, ошибка, менее либо равная 0,04, может быть сделана два раза, что необходимо учесть при подсчете вероятности:
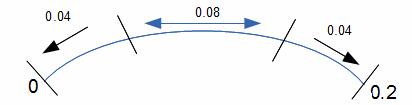
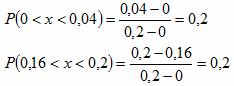
P = 0,2 + 0,2 = 0,4
Для второго случая величина ошибки может превышать 0,02 также с обеих границ деления, то есть она может быть либо больше 0,02, либо меньше 0,18.
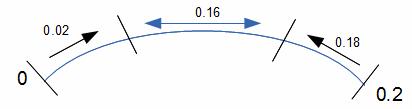
Тогда вероятность появления такой ошибки:
Пример №2. Предполагалось, что о стабильности экономической обстановки в стране (отсутствии войн, стихийных бедствий и т. д.) за последние 50 лет можно судить по характеру распределения населения по возрасту: при спокойной обстановке оно должно быть равномерным. В результате проведенного исследования, для одной из стран были получены следующие данные.
| Возрастной интервал | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Доля населения | 0,14 | 0,09 | 0,10 | 0,08 | 0,16 | 0,13 | 0,12 | 0,18 |
| Группы | Середина интервала, xi | Кол-во, fi | xi * fi | Накопленная частота, S | |x - xср|*f | (x - xср)2*f | Частота, fi/n |
| 0 - 10 | 5 | 0.14 | 0.7 | 0.14 | 5.32 | 202.16 | 0.14 |
| 10 - 20 | 15 | 0.09 | 1.35 | 0.23 | 2.52 | 70.56 | 0.09 |
| 20 - 30 | 25 | 0.1 | 2.5 | 0.33 | 1.8 | 32.4 | 0.1 |
| 30 - 40 | 35 | 0.08 | 2.8 | 0.41 | 0.64 | 5.12 | 0.08 |
| 40 - 50 | 45 | 0.16 | 7.2 | 0.57 | 0.32 | 0.64 | 0.16 |
| 50 - 60 | 55 | 0.13 | 7.15 | 0.7 | 1.56 | 18.72 | 0.13 |
| 60 - 70 | 65 | 0.12 | 7.8 | 0.82 | 2.64 | 58.08 | 0.12 |
| 70 - 80 | 75 | 0.18 | 13.5 | 1 | 5.76 | 184.32 | 0.18 |
| 1 | 43 | 20.56 | 572 | 1 |
Средняя взвешенная
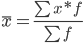
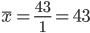
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax - Xmin
R = 70 - 0 = 70
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
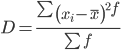
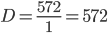
Среднее квадратическое отклонение.
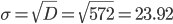
Каждое значение ряда отличается от среднего значения 43 не более, чем на 23.92
Проверка гипотез о виде распределения.
4. Проверка гипотезы о равномерном распределении генеральной совокупности.
Для того чтобы проверить гипотезу о равномерном распределении X,т.е. по закону: f(x) = 1/(b-a) в интервале (a,b)
надо:
1. Оценить параметры a и b - концы интервала, в котором наблюдались возможные значения X, по формулам (через знак * обозначены оценки параметров):
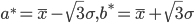
2. Найти плотность вероятности предполагаемого распределения f(x) = 1/(b* - a*)
3. Найти теоретические частоты:
n1 = nP1 = n[f(x)*(x1 - a*)] = n*1/(b* - a*)*(x1 - a*)
n2 = n3 = ... = ns-1 = n*1/(b* - a*)*(xi - xi-1)
ns = n*1/(b* - a*)*(b* - xs-1)
4. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы k = s-3, где s - число первоначальных интервалов выборки; если же было произведено объединение малочисленных частот, следовательно, и самих интервалов, то s - число интервалов, оставшихся после объединения.
Решение:
1. Найдем оценки параметров a* и b* равномерного распределения по формулам:
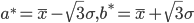
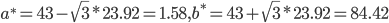
2. Найдем плотность предполагаемого равномерного распределения:
f(x) = 1/(b* - a*) = 1/(84.42 - 1.58) = 0.0121
3. Найдем теоретические частоты:
n1 = n*f(x)(x1 - a*) = 1 * 0.0121(10-1.58) = 0.1
n8 = n*f(x)(b* - x7) = 1 * 0.0121(84.42-70) = 0.17
Остальные ns будут равны:
ns = n*f(x)(xi - xi-1)
| i | ni | n*i | ni - n*i | (ni - n*i)2 | (ni - n*i)2/n*i |
| 1 | 0.14 | 0.1 | 0.0383 | 0.00147 | 0.0144 |
| 2 | 0.09 | 0.12 | -0.0307 | 0.000943 | 0.00781 |
| 3 | 0.1 | 0.12 | -0.0207 | 0.000429 | 0.00355 |
| 4 | 0.08 | 0.12 | -0.0407 | 0.00166 | 0.0137 |
| 5 | 0.16 | 0.12 | 0.0393 | 0.00154 | 0.0128 |
| 6 | 0.13 | 0.12 | 0.0093 | 8.6E-5 | 0.000716 |
| 7 | 0.12 | 0.12 | -0.000701 | 0 | 4.0E-6 |
| 8 | 0.18 | 0.17 | 0.00589 | 3.5E-5 | 0.000199 |
| Итого | 1 | 0.0532 |
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры a и b).
Kkp = 11.07050; Kнабл = 0.0532
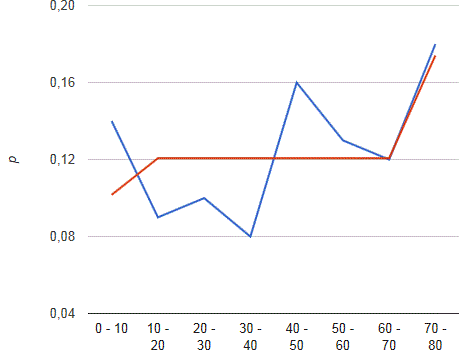
Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют равномерный закон.
| xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| mi | 26 | 21 | 18 | 32 | 26 | 26 | 31 |
Проверьте гипотезу о том, что данная случайная величина имеет равномерное дискретное распределение. Уровень значимости a= 0,1.
Решение. Выдвигаем основную и альтернативную гипотезы:
H0: данная случайная величина имеет равномерное дискретное распределение;
H1: данная случайная величина не имеет равномерное дискретное распределение.
Считаем, что данное распределение является равномерным дискретным. Тогда вероятности всех значений этой величины одинаковы и равны
(k – количество значений случайной величины). Умножаем эту вероятности на объём выборки (n = 180) и получаем теоретические частоты mi’ = 0,1429×180 = 25,714 (они также будут все одинаковыми).
Заполняем два оставшихся столбца и находим суммы по столбцам.
| xi | mi | pi | mi’ | mi– mi’ |  |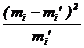
| 1 | 26 | 0,1429 | 25,714 | 0,286 | 0,003181 |
| 2 | 21 | 0,1429 | 25,714 | -4,714 | 0,864191 |
| 3 | 18 | 0,1429 | 25,714 | -7,714 | 2,31414 |
| 4 | 32 | 0,1429 | 25,714 | 6,286 | 1,536665 |
| 5 | 26 | 0,1429 | 25,714 | 0,286 | 0,003181 |
| 6 | 26 | 0,1429 | 25,714 | 0,286 | 0,003181 |
| 7 | 31 | 0,1429 | 25,714 | 5,286 | 1,086637 |
| S | 180 | 1 | 180 | 0 | 5,811 |
Последняя сумма соответствует искомому критерию Χнабл2=5,811.
Данная выборка разбита на l = 7 интервалов. Для дискретного равномерного распределения р = 0 (подбираемых параметра нет). Поэтому число степеней свободы в данном случае k = l-p - 1 = 7 - 0 - 1 = 6. При уровне значимости a= 0,1 и найденному числу степеней свободы из таблицы критических точек распределения Χ2 находим значение критерия Χкр2=10.64.
Т.к. Χнабл2 < Χкр 2, то нулевая гипотеза принимается: выборочные данные не противоречат тому, что распределение данной случайной величины является равномерным дискретным.
Пример №4. Игральную кость бросили 600 раз и результаты наблюдений записали в виде статистического ряда. Случайная величина X – число выпавших очков, ni – частота выпадения i очков, где i= 1, 2, 3, 4, 5, 6. На уровне значимости α = 0,01 проверить гипотезу о симметричности игральной кости.
Пример №5. Заданная непрерывная случайная величина Х равномерно распределена в интервале (α, β).
Найти:
1) Числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение.
2) интегральную функцию распределения.
3) Сделать графики дифференциальной и интегральной функций распределения.
α=3, β=8
