Уравнение парной регрессии. Руководство к решению задач
Задание 1. При исследовании 8 магазинов получены следующие данные.
| Наблюдение | Объем товарооборота, млн. руб. | Число работников |
| 1 | 0,5 | 73 |
| 2 | 0,7 | 85 |
| 3 | 0,9 | 102 |
| 4 | 1,1 | 115 |
| 5 | 1,4 | 122 |
| 6 | 1,4 | 126 |
| 7 | 1,7 | 134 |
| 8 | 1,9 | 147 |
Построить регрессионную модель зависимости объема товарооборота от числа работников. Проверить значимость модели и коэффициентов модели. Рассчитать коэффициент эластичности и дать ему экономическую интерпретацию. Построить 95% доверительный интервал для оценки объема товарооборота отдельного магазина со 100 работниками.
Решение:
Для решения используем сервис «Уравнение парной регрессии». Исходные данные можно ввести вручную (при этом необходимо указать параметр Количество строк: 8) или вставить данные из Excel. Уровень значимости устанавливаем как 0.05.
Поскольку необходимо найти зависимость объема товарооборота от числа работников, то в качестве Y – принимаем Объем товарооборота, X - Число работников.

Рисунок 1 – Вставка исходных данных из Excel
На следующем шаге определяем параметры отчета: t-статистика. Критерий Стьюдента, F-статистика. Критерий Фишера.
Получаем таблицу вида:
| x | y | x2 | y2 | x•y | y(x) | (yi-ycp)2 | (y-y(x))2 | (xi-xcp)2 | |y - yx|:y |
| 73 | 0.5 | 5329 | 0.25 | 36.5 | 0.43 | 0.49 | 0.004832 | 1600 | 0.14 |
| 85 | 0.7 | 7225 | 0.49 | 59.5 | 0.66 | 0.25 | 0.001495 | 784 | 0.0552 |
| 102 | 0.9 | 10404 | 0.81 | 91.8 | 0.99 | 0.09 | 0.007812 | 121 | 0.0982 |
| 115 | 1.1 | 13225 | 1.21 | 126.5 | 1.24 | 0.01 | 0.0192 | 4 | 0.13 |
| 122 | 1.4 | 14884 | 1.96 | 170.8 | 1.37 | 0.04 | 0.000721 | 81 | 0.0192 |
| 126 | 1.4 | 15876 | 1.96 | 176.4 | 1.45 | 0.04 | 0.002509 | 169 | 0.0358 |
| 134 | 1.7 | 17956 | 2.89 | 227.8 | 1.6 | 0.25 | 0.009217 | 441 | 0.0565 |
| 147 | 1.9 | 21609 | 3.61 | 279.3 | 1.85 | 0.49 | 0.002108 | 1156 | 0.0242 |
| 904 | 9.6 | 106508 | 13.18 | 1168.6 | 9.6 | 1.66 | 0.0479 | 4356 | 0.55 |
здесь столбцы 1-5 используются для вычисления остальных столбцов таблицы.
y(x) – определяется по найденным коэффициентам регрессии как y(x) = bx + a и используется для вычисления столбцов 8 и 10.
(yi-ycp)2, (y-y(x))2– значения столбцов используются для вычисления коэффициента детерминации R2(п. 1.5. и 2.5.2 отчета).
(xi-xcp)2 – используется для построения доверительного интервала зависимой переменой (п.2.4. отчета)
|y - yx|:y – используется при вычислении ошибки аппроксимации.
Если вычисление каких-либо коэффициентов не запланировано заданием, соответствующие столбцы можно удалить (обычно это столбцы 9 и 10).
Регрессионная модель имеет вид: y = 0.0192x - 0.97
Автоматически строится поле корреляции.
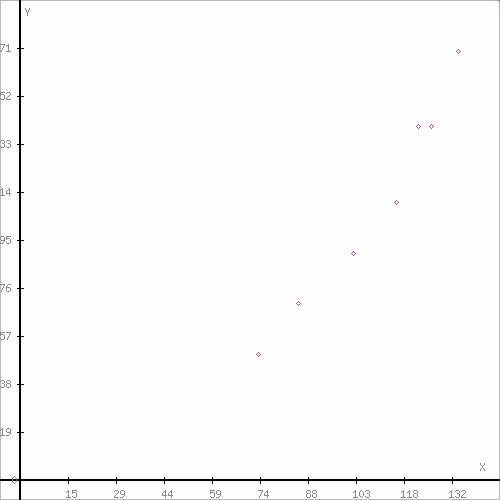
Рисунок 2 – Поле корреляции
Скачать решение
Задание 2. Имеются следующие данные о связи между произведенной продукцией (в отпускных ценах) и переработкой сырья по 12 предприятиям:
| Номер предприятия | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Валовая продукция, млрд р. | 2,4 | 2,8 | 3,4 | 3,6 | 4,0 | 4,4 | 4,8 | 5,3 | 5,5 | 6,0 | 6,2 | 6,5 |
| Переработано сырья, тыс. ц | 0,6 | 0,9 | 1,2 | 0,8 | 1,4 | 1,8 | 1,6 | 2,0 | 2,4 | 2,7 | 2,9 | 3,2 |
Составьте линейное уравнение регрессии, вычислите параметры и оцените тесноту корреляционной связи.
Решение:
В качестве факторной переменной X принимаем параметр Переработано сырья (тыс. ц), в качестве зависимой переменной Y - Валовая продукция ( млрд р.). Подготовим данные для вставки из Excel. Для этого скопируем таблицу в Excel и транспонируем с помощью функции ТРАНСП.
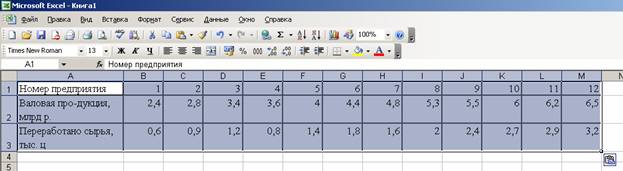
Рисунок 3 – Подготовка данных для обработки
В ячейку А5 записываем формулу
=ТРАНСП(A1:M3)
Выделяем диапазон А5:С17 и нажимаем F2, а затем сочетание клавиш Enter+Shift+Ctrl.
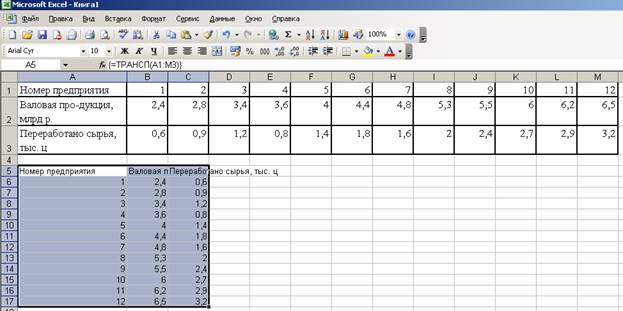
Просмотреть вставку данных из Excel Ниже представлена видеоинструкция по заполнению данных.
Оценка тесноты корреляционной связи производится в п.1.1 отчета.
Скачать решение
Задание 3. По данным задачи 6 для изучения тесноты связи между средними товарными запасами (результативный признак Y) и оборотом розничной торговли (факторный признак) вычислите эмпирическое корреляционное отношение. Сделайте выводы.
Решение:
Эмпирическое корреляционное отношение рассчитывается в п.1.5.
Задание 4. Имеются выборочные данные по однородным предприятиям: энерговооруженность труда одного рабочего (кВт/час) и выпуск готовой продукции (шт). Определить:
- Факторные и результативные признаки.
- Провести исследование взаимосвязи энерговооруженности и выпуска готовой продукции.
- Найти коэффициент регрессии и построить уравнение регрессии.
- Построить графики практической и теоретической линии регрессии.
- Определить форму связи и измерить тесноту связи.
- Провести оценку адекватности регрессионной модели с помощью критерия Фишера.
В данном случае в качестве факторного признака выступает энерговооруженность труда одного рабочего (X), а результативный признак - выпуск готовой продукции (Y).
Коэффициент регрессии для уравнения y = bx + a определяется значением b (см. п. 1.2 отчета или расчеты на основе МНК). Графики практической и теоретической линии регрессии удобней строить средствами Excel. Форму связи можно определить исходя из графика. Измерение тесноты связи и ее анализ см. в п.1.2 отчета.
Оценка адекватности регрессионной модели проводится в п.2.5 (раздел №2: F-статистика. Критерий Фишера).
Задание 4. Экономист, изучая зависимость уровня Y (тыс. руб.) издержек обращения от объема X (тыс. руб.) товарооборота, обследовал по 10 магазинов, торгующих одинаковым ассортиментом товаров в 5 районах. Полученные данные отражены в таблице 1. Задание. Для каждого из районов (в каждой задаче) требуется:
- найти коэффициенты корреляции между X и Y;
- построить регрессионные функции линейной зависимости Y = a + b*X фактора Y от фактора X и исследовать их на надежность по критерию Фишера при уровне значимости 0.05;
- найти коэффициент эластичности Y по X при среднем значении X;
- определить надежность коэффициентов регрессии по критерию Стьюдента:
- найти доверительные интервалы для коэффициентов регрессии;
- построить график регрессионной функции и диаграмму рассеяния;
- используя полученное уравнение линейной регрессии, оценить ожидаемое среднее значение признака Y при X = 130 тыс. руб.
Решение:
Уровень значимости оставляем по умолчанию (0.05), значение зависимой переменной устанавливаем как 130. Вставляем данные через кнопку Вставить из Excel.
Включать в отчет: t-статистика. Критерий Стьюдента, F-статистика. Критерий Фишера.
