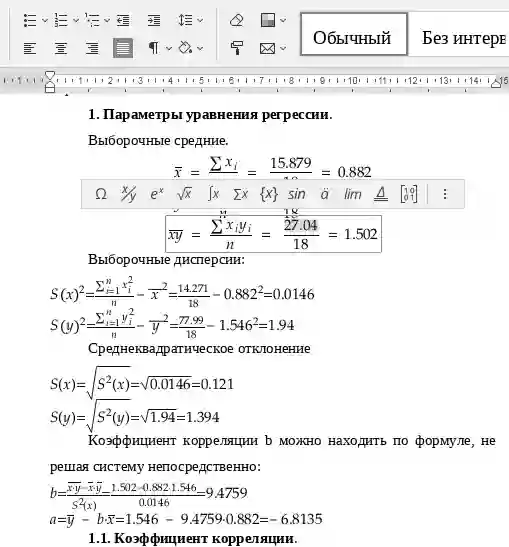
Инструкция. Введите исходные данные. Полученное решение сохраняется в файле Word (см. пример нахождения уравнения регрессии). Также автоматически создается шаблон решения в Excel. Подробнее.
Исходные данные можно вставить (X - первый столбец, Y - второй столбец):

вручную (см. пример заполнения).
из текстового файла. Для txt файлов в качестве разделителя выступает знак табуляции, для csv файлов - запятая.
из Excel.

При количестве данных больше 1000, создается только шаблон решения в MS Excel. Если требуется построить сразу несколько уравнений регрессии и найти лучшее из них, то можно воспользоваться сервисом Регрессионный анализ в Excel.
Для получения обратного уравнения регрессии x=by+a, достаточно вставить данные в обратном порядке (первый столбец Y, второй столбец X).
Примечание: ограничить однородную совокупность единиц, устранив аномальные объекты наблюдения можно через метод Ирвина или по правилу трех сигм (устранить те единицы, для которых значение объясняющего фактора отклоняется от среднего более, чем на утроенное среднеквадратичное отклонение).
Для получения обратного уравнения регрессии x=by+a, достаточно вставить данные в обратном порядке (первый столбец Y, второй столбец X).

см. также сервис Корреляционная таблица.

Здесь будет отображаться решение.

Скачать пример оформления

Типовые задания (см. также нелинейная регрессия)

Типовые задания
Исследуется зависимость производительности труда y от уровня механизации работ x (%) по данным 14 промышленных предприятий. Статистические данные приведены в таблице.
Требуется:
1) Найти оценки параметров линейной регрессии у на х. Построить диаграмму рассеяния и нанести прямую регрессии на диаграмму рассеяния.
2) На уровне значимости α=0.05 проверить гипотезу о согласии линейной регрессии с результатами наблюдений.
3) С надежностью γ=0.95 найти доверительные интервалы для параметров линейной регрессии.

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

Уравнение регрессии

Назначение сервиса. С помощью сервиса в онлайн режиме можно найти:

параметры уравнения линейной регрессии y=a+bx, линейный коэффициент корреляции с проверкой его значимости;
тесноту связи с помощью показателей корреляции и детерминации, МНК-оценку, статическую надежность регрессионного моделирования с помощью F-критерия Фишера и с помощью t-критерия Стьюдента, доверительный интервал прогноза для уровня значимости α

В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 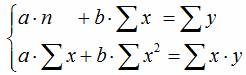. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel

Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.

Пример. Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели - определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x, т. е. модель вида:

y(x) = f^{^}(x),

где y – зависимая переменная (результативный признак); x – независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменными x и y нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина y складывается из двух слагаемых:

y = y_x + ε,

где y – фактическое значение результативного признака; y_x – теоретическое значение результативного признака, найденное исходя из уравнения регрессии; ε – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Графически покажем регрессионную зависимость между выработкой продукции на одного работника и удельного веса рабочих высокой квалификации.
$графическое изображение регрессионной зависимости$
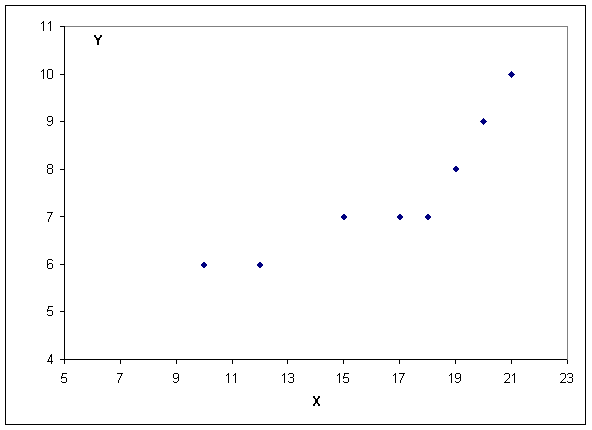
3-й этап (параметризация) – собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в неё связей между переменными. Выбор вида функциональной зависимости в уравнении регрессии называется параметризацией модели. Выбираем уравнение парной регрессии, т.е. на конечный результат y будет влиять только один фактор.
4-й этап (информационный) – сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показателей. Выборка состоит из 10 предприятий отрасли.
5-й этап (идентификация модели) – оценивание неизвестных параметров модели по имеющимся статистическим данным.
Чтобы определить параметры модели, используем МНК - метод наименьших квадратов. Система нормальных уравнений будет выглядеть следующим образом:
a•n + b∑x = ∑y
a∑x + b∑x² = ∑y•x
Для расчета параметров регрессии построим расчетную таблицу (табл. 1).

x	y	x²	y²	x • y
10	6	100	36	60
12	6	144	36	72
15	7	225	49	105
17	7	289	49	119
18	7	324	49	126
19	8	361	64	152
19	8	361	64	152
20	9	400	81	180
20	9	400	81	180
21	10	441	100	210
171	77	3045	609	1356

Данные берем из таблицы 1 (последняя строка), в итоге имеем:
10a + 171 b = 77
171 a + 3045 b = 1356
Эту СЛАУ решаем методом Крамера или методом обратной матрицы.
Получаем эмпирические коэффициенты регрессии: b = 0.3251, a = 2.1414
Эмпирическое уравнение регрессии имеет вид:
y = 0.3251 x + 2.1414
6-й этап (верификация модели) – сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных.
Анализ проводим с помощью проверки адекватности модели и с помощью статистической значимости параметров парной регрессии.

Оценка параметров уравнения регреcсии

Проверить значимость параметров уравнения регрессии можно, используя t-статистику.

Задание:
По группе предприятий, выпускающих один и тот же вид продукции, рассматриваются функции издержек:
y = α + βx;
y = α x^β;
y = α β^x;
y = α + β / x;
где y – затраты на производство, тыс. д. е.
x – выпуск продукции, тыс. ед.

Требуется:
1. Построить уравнения парной регрессии y от x:

линейное;
степенное;
показательное;
равносторонней гиперболы.

2. Рассчитать линейный коэффициент парной корреляции и коэффициент детерминации. Сделать выводы.
3. Оценить статистическую значимость уравнения регрессии в целом.
4. Оценить статистическую значимость параметров регрессии и корреляции.
5. Выполнить прогноз затрат на производство при прогнозном выпуске продукции, составляющем 195 % от среднего уровня.
6. Оценить точность прогноза, рассчитать ошибку прогноза и его доверительный интервал.
7. Оценить модель через среднюю ошибку аппроксимации.

Решение:

1. Уравнение имеет вид y = α + βx
1. Параметры уравнения регрессии.
Средние значения

Дисперсия

Среднеквадратическое отклонение

Коэффициент корреляции

Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии

Коэффициент детерминации
R²=0.94² = 0.89, т.е. в 88.9774 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая

x	y	x²	y²	x ∙ y	y(x)	(y-y)²	(y-y(x))²	(x-x_p)²
78	133	6084	17689	10374	142.16	115.98	83.83	1
82	148	6724	21904	12136	148.61	17.9	0.37	9
87	134	7569	17956	11658	156.68	95.44	514.26	64
79	154	6241	23716	12166	143.77	104.67	104.67	0
89	162	7921	26244	14418	159.9	332.36	4.39	100
106	195	11236	38025	20670	187.33	2624.59	58.76	729
67	139	4489	19321	9313	124.41	22.75	212.95	144
88	158	7744	24964	13904	158.29	202.51	0.08	81
73	152	5329	23104	11096	134.09	67.75	320.84	36
87	162	7569	26244	14094	156.68	332.36	28.33	64
76	159	5776	25281	12084	138.93	231.98	402.86	9
115	173	13225	29929	19895	201.86	854.44	832.66	1296
		0	0	0	16.3	20669.59	265.73	6241
1027	1869	89907	294377	161808	1869	25672.31	2829.74	8774

Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(1) = 4.01*1 + 99.18 = 103.19 y(2) = 4.01*2 + 99.18 = 107.2 ... ... ...

2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл
T_табл (n-m-1;α/2) = (11;0.05/2) = 1.796
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически - значим.

Анализ точности определения оценок коэффициентов регрессии

S_a = 0.1712
Доверительные интервалы для зависимой переменной

Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-20.41;56.24)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика

Статистическая значимость коэффициента регрессии a подтверждается

Статистическая значимость коэффициента регрессии b не подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (t_табл=1.796):
(a - t_табл·S_a; a + t_табл·S_a)
(1.306;1.921)
(b - t_табл·S_b; b + t_табл·S_b)
(-9.2733;41.876)
где t = 1.796
2) F-статистики

Fkp = 4.84
Поскольку F > Fkp, то коэффициент детерминации статистически значим.

Уравнение регрессии

Оценка параметров уравнения регреcсии

Правила ввода данных

Поиск

Процесс

Сообщение