Пример нахождения статистической значимости коэффициентов регрессии
С помощью МНК мы получили лишь оценки параметров уравнения регрессии, которые характерны для конкретного статистического наблюдения (конкретного набора значений x и y). Если оценку параметров произвести по данным другого статистического наблюдения (другому набору значений x и y), то получим другие численные значенияЧтобы проверить, значимы ли параметры, т.е. значимо ли они отличаются от нуля для генеральной совокупности используют статистические методы проверки гипотез.
В качестве основной (нулевой) гипотезы выдвигают гипотезу о незначимом отличии от нуля параметра или статистической характеристики в генеральной совокупности. Наряду с основной (проверяемой) гипотезой выдвигают альтернативную (конкурирующую) гипотезу о неравенстве нулю параметра или статистической характеристики в генеральной совокупности. В случае если основная гипотеза окажется неверной, мы принимаем альтернативную. Для проверки этой гипотезы используется t-критерий Стьюдента.
Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактическим) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (которые обычно приводятся в конце учебников и практикумов по статистике или эконометрике). Табличное значение определяется в зависимости от уровня значимости (a) и числа степеней свободы, которое в случае линейной парной регрессии равно (n-2), n-число наблюдений.
Если фактическое значение t-критерия больше табличного (по модулю), то основную гипотезу отвергают и считают, что с вероятностью (1-a) параметр или статистическая характеристика в генеральной совокупности значимо отличается от нуля.
Если фактическое значение t-критерия меньше табличного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр или статистическая характеристика в генеральной совокупности незначимо отличается от нуля при уровне значимости a.
Для параметра b критерий проверки имеет вид:
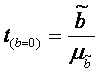 ,
,
где
μδ – стандартная ошибка коэффициента регрессии.
Для линейного парного уравнения регрессии стандартная ошибка коэффициента вычисляется по формуле:
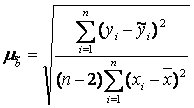 .
.
Числитель в этой формуле может быть рассчитан через коэффициент детерминации и общую дисперсию признака-результата: 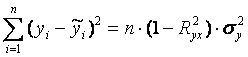 .
.
Для параметра a критерий проверки гипотезы о незначимом отличии его от нуля имеет вид:
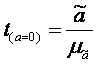 ,
,
где ![]() - оценка параметра регрессии, полученная по наблюдаемым данным;
- оценка параметра регрессии, полученная по наблюдаемым данным;
μa – стандартная ошибка параметра a.
Для линейного парного уравнения регрессии:
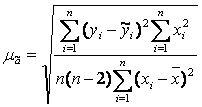 .
.
Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции в генеральной совокупности используют следующий критерий:
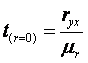 , где ryx - оценка
коэффициента корреляции, полученная по наблюдаемым данным;
mr – стандартная ошибка коэффициента корреляции ryx.
, где ryx - оценка
коэффициента корреляции, полученная по наблюдаемым данным;
mr – стандартная ошибка коэффициента корреляции ryx.
Для линейного парного уравнения регрессии:
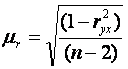 .
.
В парной линейной регрессии между наблюдаемыми значениями критериев существует взаимосвязь: t ( b =0) = t (r=0).
Пример №1. Уравнение имеет вид y=ax+b
1. Параметры уравнения регрессии.
Средние значения
Дисперсия
Коэффициент корреляции
Уравнение регрессии
Коэффициент детерминации
R 2= 0.73 2 = 0.54, т.е. в 54% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - средняя.
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y-y cp) 2 | (y-y(x))2 | (x-x p) 2 |
| 69 | 124 | 4761 | 15376 | 8556 | 128.48 | 491.36 | 20.11 | 367.36 |
| 83 | 133 | 6889 | 17689 | 11039 | 141.4 | 173.36 | 70.56 | 26.69 |
| 92 | 146 | 8464 | 21316 | 13432 | 149.7 | 0.03 | 13.71 | 14.69 |
| 97 | 153 | 9409 | 23409 | 14841 | 154.32 | 46.69 | 1.73 | 78.03 |
| 88 | 138 | 7744 | 19044 | 12144 | 146.01 | 66.69 | 64.21 | 0.03 |
| 93 | 159 | 8649 | 25281 | 14787 | 150.63 | 164.69 | 70.13 | 23.36 |
| 74 | 145 | 5476 | 21025 | 10730 | 133.1 | 1.36 | 141.68 | 200.69 |
| 79 | 152 | 6241 | 23104 | 12008 | 137.71 | 34.03 | 204.21 | 84.03 |
| 105 | 168 | 11025 | 28224 | 17640 | 161.7 | 476.69 | 39.74 | 283.36 |
| 99 | 154 | 9801 | 23716 | 15246 | 156.16 | 61.36 | 4.67 | 117.36 |
| 85 | 127 | 7225 | 16129 | 10795 | 143.25 | 367.36 | 263.91 | 10.03 |
| 94 | 155 | 8836 | 24025 | 14570 | 151.55 | 78.03 | 11.91 | 34.03 |
| 1058 | 1754 | 94520 | 258338 | 155788 | 1754 | 1961.67 | 906.57 | 1239.67 |
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически - значим.
Анализ точности определения оценок коэффициентов регрессии
S a = 0.2704
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (3.41>1.812).
Статистическая значимость коэффициента регрессии b подтверждается (2.7>1.812).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (tтабл=1.812):
(a - tтабл·S a; a + tтабл·Sa)
(0.4325;1.4126)
(b - tтабл·S b; b + tтабл·Sb)
(21.3389;108.3164)
2) F-статистики
Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.
Перейти к онлайн решению своей задачи
Пример №2. По территориям региона приводятся данные за 199Х г.;
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
1. Построить линейное уравнение парной регрессии у от х.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимума х, составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Решение находим с помощью калькулятора.
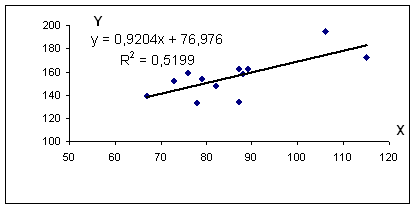
Использование графического метода .
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс - индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε - случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β - используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
12a+1027b=1869
1027a+89907b=161808
Из первого уравнения выражаем а и подставим во второе уравнение. Получаем b = 0.92, a = 76.98
Уравнение регрессии: y = 0.92 x + 76.98
1. Параметры уравнения регрессии.
Выборочные средние.
Выборочные дисперсии:
Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;
В нашем примере связь между среднедневной заработной платы и среднедушевым прожиточным минимумом высокая и прямая.
1.2. Уравнение регрессии (оценка уравнения регрессии).
Коэффициентам уравнения линейной регрессии можно придать экономический смысл.
Коэффициент b = 0.92 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 руб. среднедушевого прожиточного минимума в день среднедневная заработная плата повышается в среднем на 0.92.
Коэффициент a = 76.98 формально показывает прогнозируемый уровень Среднедневная заработная плата , но только в том случае, если х=0 находится близко с выборочными значениями.
Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между среднедневной заработной платы и среднедушевого прожиточного минимума в день определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь прямая.
Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета - коэффициенты. Коэффициент эластичности находится по формуле:
Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
Коэффициент эластичности меньше 1. Следовательно, при изменении среднедушевого прожиточного минимума в день на 1%, среднедневная заработная плата изменится менее чем на 1%. Другими словами - влияние среднедушевого прожиточного минимума Х на среднедневную заработную плату Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R2= 0.722 = 0.5199, т.е. в 51.99 % случаев изменения среднедушевого прожиточного минимума х приводят к изменению среднедневной заработной платы y. Другими словами - точность подбора уравнения регрессии - средняя. Остальные 48.01% изменения среднедневной заработной платы Y объясняются факторами, не учтенными в модели.
| x | y | x2 | y2 | x·y | y(x) | (yi-y)2 | (y-y(x))2 | (xi-x)2 | |y-yx|:y |
| 78 | 133 | 6084 | 17689 | 10374 | 148,77 | 517,56 | 248,7 | 57,51 | 0,1186 |
| 82 | 148 | 6724 | 21904 | 12136 | 152,45 | 60,06 | 19,82 | 12,84 | 0,0301 |
| 87 | 134 | 7569 | 17956 | 11658 | 157,05 | 473,06 | 531,48 | 2,01 | 0,172 |
| 79 | 154 | 6241 | 23716 | 12166 | 149,69 | 3,06 | 18,57 | 43,34 | 0,028 |
| 89 | 162 | 7921 | 26244 | 14418 | 158,89 | 39,06 | 9,64 | 11,67 | 0,0192 |
| 106 | 195 | 11236 | 38025 | 20670 | 174,54 | 1540,56 | 418,52 | 416,84 | 0,1049 |
| 67 | 139 | 4489 | 19321 | 9313 | 138,65 | 280,56 | 0,1258 | 345,34 | 0,0026 |
| 88 | 158 | 7744 | 24964 | 13904 | 157,97 | 5,06 | 0,0007 | 5,84 | 0,0002 |
| 73 | 152 | 5329 | 23104 | 11096 | 144,17 | 14,06 | 61,34 | 158,34 | 0,0515 |
| 87 | 162 | 7569 | 26244 | 14094 | 157,05 | 39,06 | 24,46 | 2,01 | 0,0305 |
| 76 | 159 | 5776 | 25281 | 12084 | 146,93 | 10,56 | 145,7 | 91,84 | 0,0759 |
| 115 | 173 | 13225 | 29929 | 19895 | 182,83 | 297,56 | 96,55 | 865,34 | 0,0568 |
| 1027 | 1869 | 89907 | 294377 | 161808 | 1869 | 3280,25 | 1574,92 | 2012,92 | 0,6902 |
2.1. Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=10 находим tкрит:
tкрит = (10;0.05) = 1.812
где m = 1 - количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим.
В парной линейной регрессии t2r = t2b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
S2y = 157.4922 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
12.5496 - стандартная ошибка оценки (стандартная ошибка регрессии).
S a - стандартное отклонение случайной величины a.
Sb - стандартное отклонение случайной величины b.
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bxp ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 94
(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (10;0.05) = 1.812
Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 3.1793 > 1.812, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b - tкрит Sb; b + tкрит Sb)
(0.9204 - 1.812·0.2797; 0.9204 + 1.812·0.2797)
(0.4136;1.4273)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a-ta)
(76.9765 - 1.812·24.2116; 76.9765 + 1.812·24.2116)
(33.1051;120.8478)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
