Проверка наличия аномальных наблюдений методом Ирвина
Онлайн калькулятор предназначен для проверки наличия аномальных наблюдений с помощью критерия Ирвина и по правилутрех сигм. Значения λ в зависимости от t=1,2,...,10 представлены в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| λ | - | 0,38 | 0,77 | 0,51 | 0,89 | 0,77 | 0,64 | 0,77 | 0,26 | 0,38 |
Инструкция. Укажите количество данных (количество строк), нажмите Далее. Полученное решение сохраняется в файле Word.
Пример. Проверить ряд на наличие выбросов методом Ирвина, сгладить метод простой скользящей средней с интервалом сглаживания 3, методом экспоненциального сглаживания (α = 0,1), представить результаты сглаживания графически, определите для ряда трендовую модель в виде полинома первой степени (линейную модель), дайте точечный и интервальный прогноз на три шага вперед.
Решение.
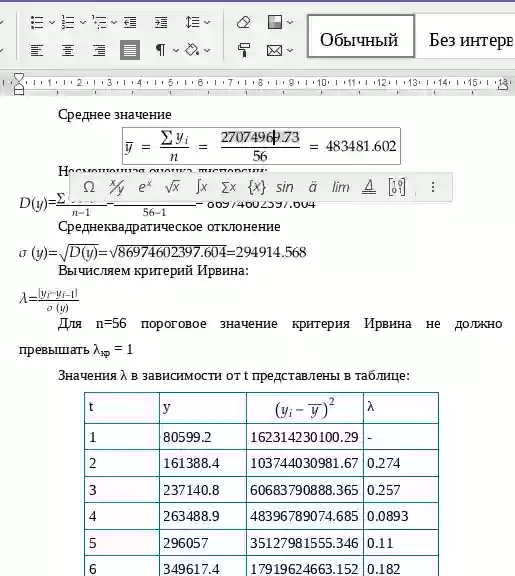
Среднее значение
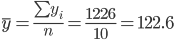
Несмещенная оценка дисперсии: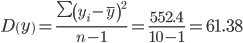
Среднеквадратическое отклонение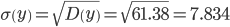
Вычисляем критерий Ирвина: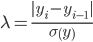
Для n=10 порогове значение критерия Ирвина не должно превышать λкр = 1.5
Значения λ в зависимости от t представлены в таблице:
| t | y | (yi-yср)2 | λ |
| 1 | 115 | 57.76 | - |
| 2 | 112 | 112.36 | 0.38 |
| 3 | 118 | 21.16 | 0.77 |
| 4 | 122 | 0.36 | 0.51 |
| 5 | 115 | 57.76 | 0.89 |
| 6 | 121 | 2.56 | 0.77 |
| 7 | 126 | 11.56 | 0.64 |
| 8 | 132 | 88.36 | 0.77 |
| 9 | 134 | 129.96 | 0.26 |
| 10 | 131 | 70.56 | 0.38 |
| 1226 | 552.4 |