Пример нахождения доверительных интервалов коэффициентов регрессии
В таблице 5 представлена динамика российского нефтяного экспорта и цены нефти марки 11га1з в 1997-2003 гг.Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Постройте уравнение зависимости экспорта нефти от цены на нефть.
3. Рассчитайте среднюю ошибку аппроксимации и коэффициент детерминации. Оценить статистическую значимость параметров регрессии и уравнения в целом.
4. Оцените полученные результаты, выводы оформите в аналитической записке.
Таблица 5
|
Годы |
Цена нефти марки Urals (Россия), долл/барр. |
Экспорт нефти и нефтепродуктов, млн.т. |
|
1997 |
18,33 |
60,6 |
|
1998 |
11,83 |
53,8 |
|
1999 |
17,30 |
56,9 |
|
2000 |
26,63 |
61,9 |
|
2001 |
22,97 |
70,8 |
|
2002 |
23,73 |
75,0 |
|
2003 |
27,04 |
76,4 |
Решение:
Уравнение имеет вид y = ax + b
1. Параметры уравнения регрессии.
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент корреляции
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
Коэффициент детерминации
R2= 0.922 = 0.84, т.е. в 84% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая
| x | y | x2 | y2 | x ∙ y | y(x) | (y-y)2 | (y-y(x))2 | (x-x p)2 |
| 119 | 298.12 | 14161 | 88875.53 | 35476.28 | 219.63 | 232120.8 | 6160.56 | 24362.01 |
| 203 | 481.03 | 41209 | 231389.86 | 97649.09 | 521.16 | 89328.76 | 1610.26 | 5196.01 |
| 281 | 539.12 | 78961 | 290650.37 | 151492.72 | 801.15 | 57979.42 | 68658.51 | 35.01 |
| 305 | 653.57 | 93025 | 427153.74 | 199338.85 | 887.3 | 15961.59 | 54628.94 | 895.01 |
| 381 | 987.66 | 145161 | 975472.28 | 376298.46 | 1160.11 | 43160.41 | 29738.57 | 11218.34 |
| 363 | 1252.85 | 131769 | 1569633.12 | 454784.55 | 1095.5 | 223673.03 | 24760.35 | 7729.34 |
| 389 | 1276.88 | 151321 | 1630422.53 | 496706.32 | 1188.83 | 246980.01 | 7753.57 | 12977.01 |
| 387 | 1396.70 | 149769 | 1950770.89 | 540522.9 | 1181.65 | 380430.93 | 46248.04 | 12525.34 |
| 315 | 952.03 | 99225 | 906361.12 | 299889.45 | 923.19 | 29625.58 | 831.49 | 1593.34 |
| 217 | 619.96 | 47089 | 384350.4 | 134531.32 | 571.41 | 25583.74 | 2356.85 | 3373.67 |
| 149 | 384.40 | 22201 | 147763.36 | 57275.6 | 327.32 | 156427.5 | 3258.23 | 15897.01 |
| 192 | 516.59 | 36864 | 266865.23 | 99185.28 | 481.67 | 69336.98 | 1219.24 | 6902.84 |
| 3301 | 9358.91 | 1010755 | 8869708.45 | 2943150.82 | 9358.91 | 1570608.75 | 247224.62 | 102704.92 |
2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически - значим.
Анализ точности определения оценок коэффициентов регрессии
S a = 0.4906
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-587.75;179.86)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (7.32>1.812)
Статистическая значимость коэффициента регрессии b не подтверждается (1.46<1.812)
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (tтабл=1.812):
(a - tтабл·S a; a + tтабл·Sa)
(2.7006;4.4786)
(b - tтабл·S b; b + tтабл·Sb)
(-465.5454;50.4796)
2) F-статистики
Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.
Перейти к онлайн решению своей задачи
Доверительные интервалы для зависимой переменной
Уравнение тренда имеет вид y = at2 + bt + c1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений

Для наших данных система уравнений имеет вид (см. таблицу).
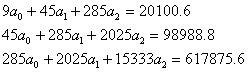
Получаем a0 = -11.37, a1 = 88.47, a2 = 2151.09
Уравнение тренда: y = -11.37t2+88.47t+2151.09
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда
Средние значения
Дисперсия
Среднеквадратическое отклонение
Индекс детерминации
т.е. в 87.35 % случаев влияет на изменение данных. Другими словами - точность подбора уравнения тренда - высокая
| t | y | t2 | y2 | x ∙ y | y(t) | (y-y cp)2 | (y-y(t))2 | (t-t p)2 | (y-y(t)) : y | t3 | t4 | t2 y |
| 1 | 2225.3 | 1 | 4951960.09 | 2225.3 | 2228.19 | 65.6099 | 8.352 | 16 | 6431.117 | 1 | 1 | 2225.3 |
| 2 | 2254.9 | 4 | 5084574.01 | 4509.8 | 2282.55 | 462.25 | 764.5225 | 9 | 62347.985 | 8 | 16 | 9019.6 |
| 3 | 2332.3 | 9 | 5439623.29 | 6996.9 | 2314.17 | 9781.21 | 328.6969 | 4 | 42284.599 | 27 | 81 | 20990.7 |
| 4 | 2365.8 | 16 | 5597009.64 | 9463.2 | 2323.05 | 17529.76 | 1827.5625 | 1 | 101137.95 | 64 | 256 | 37852.8 |
| 5 | 2295.4 | 25 | 5268861.16 | 11477 | 2309.19 | 3844 | 190.1641 | 0 | 31653.566 | 125 | 625 | 57385 |
| 6 | 2303.9 | 36 | 5307955.21 | 13823.4 | 2272.59 | 4970.25 | 980.3161 | 1 | 72135.109 | 216 | 1296 | 82940.4 |
| 7 | 2166.7 | 49 | 4694588.89 | 15166.9 | 2213.25 | 4448.89 | 2166.9025 | 4 | 100859.885 | 343 | 2401 | 106168.3 |
| 8 | 2080.4 | 64 | 4328064.16 | 16643.2 | 2131.17 | 23409 | 2577.5929 | 9 | 105621.908 | 512 | 4096 | 133145.6 |
| 9 | 2075.9 | 81 | 4309360.81 | 18683.1 | 2026.35 | 24806.25 | 2455.2025 | 16 | 102860.845 | 729 | 6561 | 168147.9 |
| 45 | 20100.6 | 285 | 44981997.26 | 98988.8 | 20100.51 | 89317.2199 | 11299.312 | 60 | 625332.964 | 4050 | 30666 | 1235751.2 |
2. Анализ точности определения оценок параметров уравнения тренда.
Анализ точности определения оценок параметров уравнения тренда
S a = 4.8518
Доверительные интервалы для зависимой переменной
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (7;0.05) = 1.895
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 6
2151.09 + 88.47*6 + -11.37*62 - 1.895*39.911 ; 2151.09 + 88.47*6 + -11.37*62 - 1.895*39.911
(-55.3814;95.8814)
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
где L - период упреждения; уn+L - точечный прогноз по модели на (n + L)-й момент времени; n - количество наблюдений во временном ряду; Sy - стандартная ошибка прогнозируемого показателя; Tтабл - табличное значение критерия Стьюдента для уровня значимости а и для числа степеней свободы, равного n — 2.
Точечный прогноз, t = 10: y(10) = -11.37*102 + 88.47* + 2151.09 = 1898.79
K1 = 247.4924
1898.79 - 247.4924 = 1651.2976 ; 1898.79 + 247.4924 = 2146.2824
t = 10: (1651.2976;2146.2824)
Точечный прогноз, t = 11: y(11) = -11.37*112 + 88.47* + 2151.09 = 1748.49
K2 = 261.9213
1748.49 - 261.9213 = 1486.5687 ; 1748.49 + 261.9213 = 2010.4113
t = 11: (1486.5687;2010.4113)
Точечный прогноз, t = 12: y(12) = -11.37*122 + 88.47* + 2151.09 = 1575.45
K3 = 278.0099
1575.45 - 278.0099 = 1297.4401 ; 1575.45 + 278.0099 = 1853.4599
t = 12: (1297.4401;1853.4599)
Точечный прогноз, t = 13: y(13) = -11.37*132 + 88.47* + 2151.09 = 1379.67
K4 = 295.4871
1379.67 - 295.4871 = 1084.1829 ; 1379.67 + 295.4871 = 1675.1571
t = 13: (1084.1829;1675.1571)
Точечный прогноз, t = 14: y(14) = -11.37*142 + 88.47* + 2151.09 = 1161.15
K5 = 314.1213
1161.15 - 314.1213 = 847.0287 ; 1161.15 + 314.1213 = 1475.2713
t = 14: (847.0287;1475.2713)
3. Проверка гипотез относительно коэффициентов линейного уравнения тренда.
1) t-статистика. Критерий Стьюдента.
Статистическая значимость коэффициента уравнения подтверждается
Статистическая значимость коэффициента тренда подтверждается
Доверительный интервал для коэффициентов уравнения тренда
Определим доверительные интервалы коэффициентов тренда, которые с надежность 95% будут следующими (tтабл=1.895):
(a - tтабл·Sa; a + tтабл·Sa)
(-20.5642;-2.1758)
(b - t табл·Sb; b + tтаблS·b)
(36.7313;140.2087)
2) F-статистика. Критерий Фишера.
Fkp = 5.32
Поскольку F > Fkp, то коэффициент детерминации статистически значим
4. Тест Дарбина-Уотсона на наличие автокорреляции остатков для временного ряда.
| y | y(x) | ei = y-y(x) | e2 | (ei - ei-1)2 |
| 2225.3 | 2228.19 | -2.89 | 8.3521 | 0 |
| 2254.9 | 2282.55 | -27.65 | 764.5225 | 613.0576 |
| 2332.3 | 2314.17 | 18.13 | 328.6969 | 2095.8084 |
| 2365.8 | 2323.05 | 42.75 | 1827.5625 | 606.1444 |
| 2295.4 | 2309.19 | -13.79 | 190.1641 | 3196.7716 |
| 2303.9 | 2272.59 | 31.31 | 980.3161 | 2034.01 |
| 2166.7 | 2213.25 | -46.55 | 2166.9025 | 6062.1796 |
| 2080.4 | 2131.17 | -50.77 | 2577.5929 | 17.8084 |
| 2075.9 | 2026.35 | 49.55 | 2455.2025 | 10064.1024 |
| 11299.3121 | 24689.8824 |
Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости a, числа наблюдений n и количества объясняющих переменных m.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5 < DW < 2.5. Для более надежного вывода целесообразно обращаться к табличным значениям.
d1 < DW и d2 < DW < 4 - d2.
