Остаточная дисперсия
Для сгруппированных данных остаточная дисперсия - средняя из внутригрупповых дисперсий: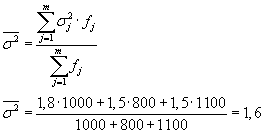
Для не сгруппированных данных остаточная дисперсия – мера точности аппроксимации, т.е. приближения линии регрессии к исходным данным:
![]()
где y(t) – прогноз по уравнению тренда; yt – исходный ряд динамики; n – количество точек; p – число коэффициентов уравнения регрессии (количество объясняющих переменных).
В этом примере она называется несмещенная оценка дисперсии.
Пример №1. Распределение рабочих трех предприятий одного объединения по тарифным разрядам характеризуется следующими данными:
| Тарифный разряд рабочего | Численность рабочих на предприятии | ||
| предприятие 1 | предприятие 2 | предприятие 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
Определить:
1. дисперсию по каждому предприятию (внутригрупповые дисперсии);
2. среднюю из внутригрупповых дисперсий;
3. межгрупповую дисперсию;
4. общую дисперсию.
Решение.
Прежде чем приступить к решению задачи необходимо выяснить, какой признак является результативным, а какой – факторным. В рассматриваемом примере результативным признаком является «Тарифный разряд», а факторным признаком – «Номер (название) предприятия».
Тогда имеем три группы (предприятия), для которых необходимо рассчитать групповую среднюю xj и внутригрупповые дисперсии σ²j:
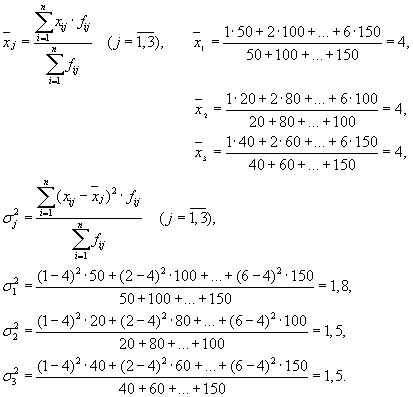
Результаты расчета сведем в таблицу:
| Предприятие | Групповая средняя, xj | Внутригрупповая дисперсия, σ²j |
| 1 2 3 | 4 4 4 | 1,8 1,5 1,5 |
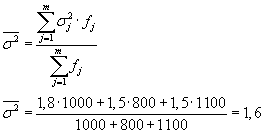
Межгрупповую дисперсию определим как:
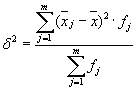
где x можно рассчитать:
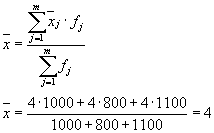
либо:
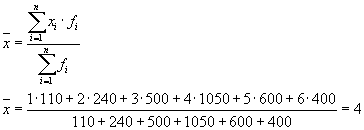
тогда:
Общая дисперсия будет равна: s2= 1,6 + 0 = 1,6.
Общую дисперсию также можно рассчитать и по одной из следующих двух формул:
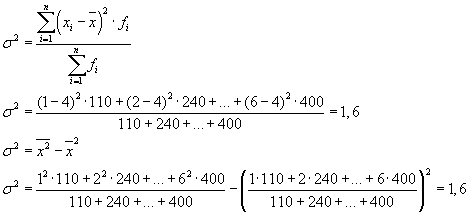
При решении практических задач часто приходится иметь дело с признаком, принимающим только два альтернативных значения. В этом случае говорят не о весе того или иного значения признака, а о его доле в совокупности. Если долю единиц совокупности, обладающих изучаемым признаком, обозначить через «р», а не обладающих – через «q», то дисперсию можно рассчитать по формуле:
s2 = p×q
Перейти к онлайн решению своей задачи
Пример №2. По данным о выработке шести рабочих бригады определить межгрупповую дисперсию и оценить влияние рабочей смены на их производительность труда, если общая дисперсия равна 12,2.
| № рабочего бригады | Выработка рабочего, шт. | |
| в I смену | во II смену | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
Решение. Исходные данные
| X | f1 | f2 | f3 | f4 | f5 | f6 | Итого |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| Итого | 31 | 33 | 37 | 37 | 40 | 38 |
Тогда имеем 6 группы, для которых необходимо рассчитать групповую среднюю и внутригрупповые дисперсии.
1. Находим средние значения каждой группы.
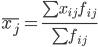
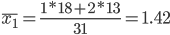
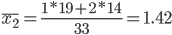
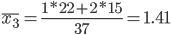
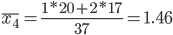
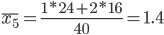
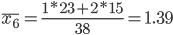
2. Находим среднее квадратическое каждой группы.
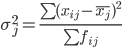
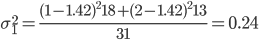
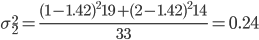
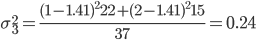
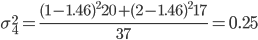
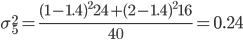
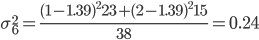
| Номер группы | Групповая средняя | Внутригрупповая дисперсия |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. Внутригрупповая дисперсия характеризует изменение (вариацию) изучаемого (результативного) признака в пределах группы под действием на него всех факторов, кроме фактора, положенного в основание группировки:
Среднюю из внутригрупповых дисперсий рассчитаем по формуле:
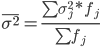
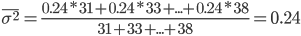
4. Межгрупповая дисперсия характеризует изменение (вариацию) изучаемого (результативного) признака под действием на него фактора (факторного признака), положенного в основание группировки.
Межгрупповую дисперсию определим как:
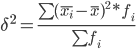
где
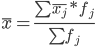
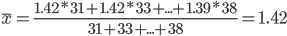
Тогда
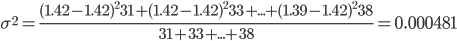
Общая дисперсия характеризует изменение (вариацию) изучаемого (результативного) признака под действием на него всех без исключения факторов (факторных признаков). По условию задачи она равна 12.2.
Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Это отношение факторной дисперсии к общей дисперсии:
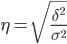
Определяем эмпирическое корреляционное отношение:
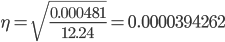
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < η < 0.3: слабая;
0.3 < η < 0.5: умеренная;
0.5 < η < 0.7: заметная;
0.7 < η < 0.9: высокая;
0.9 < η < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X слабая
Коэффициент детерминации.
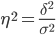
Определим коэффициент детерминации:
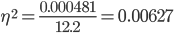
Таким образом, на 0.67% вариация обусловлена различиями между признаками, а на 99.37% – другими факторами.
Вывод: в данном случае выработка рабочих не зависит от работы в конкретную смену, т..е. влияние рабочей смены на их производительность труда не значительное и обусловлено другими факторами.
Перейти к онлайн решению своей задачи
Пример №3. На основе данных о средней заработной плате и квадратах отклонений от её величины по двум группам рабочих найти общую дисперсию, применив правило сложения дисперсий:
| Группы рабочих | Число рабочих в группах | Среднемесячная зарплата одного рабочего, тыс. руб. | Дисперсия заработной платы |
| Работающие на одном станке | 40 | 720 | 450 |
| Работающие на двух станках | 60 | 960 | 500 |
Средняя из внутригрупповых дисперсий
Межгрупповую дисперсию определим как:
Общая дисперсия будет равна:
480 + 13824 = 14304


