Частные F-критерии

Частные критерии F_x1 и F_x2 оценивают статистическую значимость включения факторов x₁ и x₂ в уравнение множественной регрессии и целесообразность включения в уравнение одного фактора после другого, т.е. F_x1 оценивает целесообразность включения в уравнение x₁ после включения в него фактора x₂.
Соответственно F_x2 указывает на целесообразность включения в модель фактора x₂ после включения фактора x₁.

где R - коэффициент множественной детерминации, r_yx1² - коэффициент множественной детерминации без учета фактора x₂, r_yx2² - коэффициент множественной детерминации без учета фактора x₁, n - количество данных, m - число переменных.
1. Расчет коэффициентов множественной линейной регрессии находим с помощью сервиса Множественная регрессия.
Система трех линейных уравнений с тремя неизвестными b₀, b₁, b₂:
∑y_i = nb₀ + b₁∑x_1i + b₂∑x_2i
∑x_1iy_i = b₀∑x_1i + b₁∑x_1i² + b₂∑x_1ix_2i
∑x_2iy_i = b₀∑x_2i + b₁∑x_1ix_2i + b₂∑x_2i²

Y	X₁	X₂	X₁²	X₂²	X₁Y	X₂Y	X₁X₂	Y²
10.3	15.8	0	249.64	0	162.74	0	0	106.09
11.2	16.4	25	268.96	625	183.68	280	410	125.44
11.42	16.83	45	283.25	2025	192.2	513.9	757.35	130.42
11.37	16.35	52	267.32	2704	185.9	591.24	850.2	129.28
11.87	17.94	65	321.84	4225	212.95	771.55	1166.1	140.9
12.5	22.78	100	518.93	10000	284.75	1250	2278	156.25
11.58	17.76	85	315.42	7225	205.66	984.3	1509.6	134.1
11.56	17.41	30	303.11	900	201.26	346.8	522.3	133.63
11.92	18.1	60	327.61	3600	215.75	715.2	1086	142.09
13.25	30	100	900	10000	397.5	1325	3000	175.56
116.97	189.37	562	35861	315844	22150.61	65737.14	106425.94	13681.98
233.94	378.74	1124	39617.08	357148	24393	72515.13	118005.49	15055.73
21.27	34.43	102.18	3601.55	32468	2217.55	6592.28	10727.77	1368.7

Для наших данных система уравнений имеет вид:
233.94 = 11 b₀ + 378.74b₁ + 1124b₂
24392.9972 = 378.74b₀ + 39617.076b₁ + 118005.49b₂
72515.13 = 1124b₀ + 118005.49b₁ + 357148b₂
Решая систему методом Крамера или методом обратной матрицы, находим:
b₀ = 0.0865
b₁ = 0.69
b₂ = -0.0253
Уравнение регрессии:
Y = 0.0865 + 0.69 X₁ -0.0253 X₂

Y	X₁	X₂	(Y_i-Y_ср)²	(X_1i-X_1ср)²	(X_2i-X_2ср)²	(Y_i-Y_ср)(X_1i-X_1ср)	(Y_i-Y_ср)(X_2i-X_2ср)	(X_1i-X_1ср)(X_2i-X_2ср)
10.3	15.8	0	120.28	347.11	10441.12	204.33	1120.66	1903.74
11.2	16.4	25	101.35	325.11	5957.03	181.52	777.01	1391.66
11.42	16.83	45	96.97	309.79	3269.76	173.32	563.08	1006.45
11.37	16.35	52	97.96	326.92	2518.21	178.95	496.66	907.33
11.87	17.94	65	88.31	271.95	1382.49	154.97	349.41	613.16
12.5	22.78	100	76.87	135.74	4.76	102.15	19.13	25.42
11.58	17.76	85	93.84	277.92	295.21	161.5	166.44	286.44
11.56	17.41	30	94.23	289.71	5210.21	165.23	700.69	1228.6
11.92	18.1	60	87.37	266.7	1779.31	152.65	394.28	688.87
13.25	30	100	64.28	19.63	4.76	35.52	17.49	9.67
116.97	189.37	562	9159.01	24006.12	211432.76	14828.09	44005.85	71243.81
233.94	378.74	1124	10080.46	26576.71	242295.64	16338.23	48610.72	79305.15
21.27	34.43	102.18	916.41	2416.06	22026.88	1485.29	4419.16	7209.56

2. Анализ качества эмпирического уравнения множественной линейной регрессии.
Построение эмпирического уравнения регрессии является начальным этапом эконометрического анализа. Первое же построенное по выборке уравнение регрессии очень редко является удовлетворительным по тем или иным характеристикам. Поэтому следующей важнейшей оценкой является проверка качества уравнения регрессии. В эконометрике принята устоявшаяся схема такой проверки, которая проводится по следующим направлениям:

проверка статистической значимости коэффициентов уравнения регрессии;
проверка общего качества уравнения регрессии;
проверка свойств данных, выполнимость которых предполагалась при оценивании уравнения (проверка выполнимости предпосылок МНК).

Прежде чем проводить анализ качества уравнения регрессии, необходимо определить дисперсии и стандартные ошибки коэффициентов, а также интервальные оценки коэффициентов.
При этом:

где m=2 – количество объясняющих переменных модели.

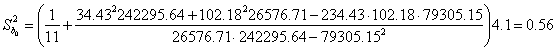
Стандартные ошибки коэффициентов:

Таблица - Расчет остатков

Y(X₁,X₂)	e_i = (Y_i-Y(X₁,X₂))	e_i²	e_i - e_i-1	(e_i - e_i-1)²
10.99	-0.69	0.48	0	0
10.77	0.43	0.18	-1.12	1.25
10.56	0.86	0.73	-0.43	0.18
10.06	1.31	1.73	-0.46	0.21
10.83	1.04	1.09	0.27	0.0723
13.28	-0.78	0.61	1.83	3.33
10.2	1.38	1.92	-2.17	4.69
11.34	0.22	0.0467	1.17	1.36
11.06	0.86	0.74	-0.64	0.41
18.26	-5.01	25.14	5.87	34.48
116.58	0.39	0.15	-5.4	29.2
233.94	0	32.81	-1.08	75.19
21.27	0	2.98	-0.0982	6.84

3. Оценка мультиколлинеарности факторов.
Парные коэффициенты корреляции.
Для y и x₁
Средние значения

Дисперсия

Среднеквадратическое отклонение

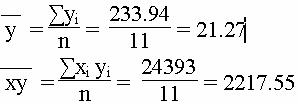
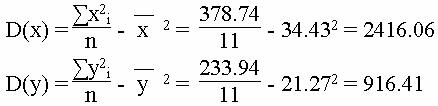
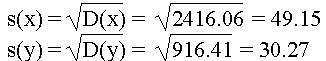
Коэффициент корреляции

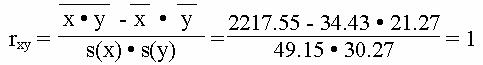
Для y и x₂
Средние значения

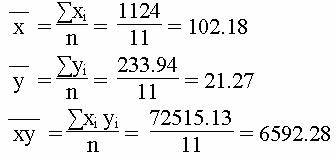
Дисперсия

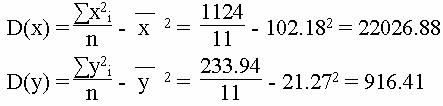
Среднеквадратическое отклонение

Коэффициент корреляции

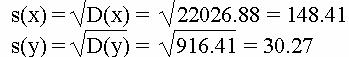
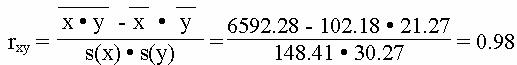
Для x₁ и x₂
Средние значения

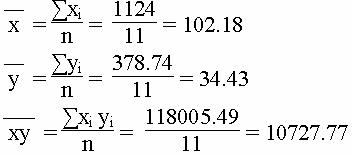
Дисперсия

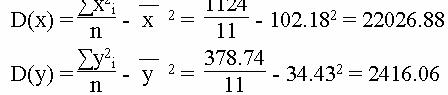
Среднеквадратическое отклонение

Коэффициент корреляции

Матрица парных коэффициентов корреляции.

-	y	x₁	x₂
y	1	0.998	0.984
x₁	0.998	1	0.988
x₂	0.984	0.988	1

4. Оценка тесноты связи.
4. Теснота связи результативного признака с факторными определятся величиной коэффициента линейной множественной корреляции и детерминации, который могут быть исчислены на основе матрицы парных коэффициентов корреляции:

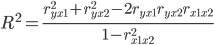
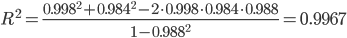
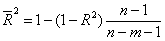
Более объективную оценку качества построенной модели дает скорректированный индекс множественной детерминации, учитывающий поправку на число степеней свободы:

где n - число наблюдений, m – число факторов.

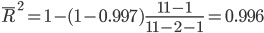
7. Проверка гипотезы о статистической значимости уравнения регрессии.
Проверка гипотезы H₀ о статистической значимости уравнения регрессии и показателя тесноты связи (R² = 0) производится по F-критерию Фишера сравнением F_факт с F_табл.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

где m – число факторов в модели.
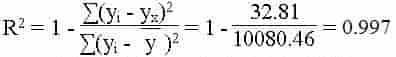
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R²=0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:

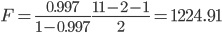
где m=2 для множественной регрессии с двумя факторами.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 2 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2-1.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k₁=2 и k₂=8, Fkp = 4.46
Поскольку фактическое значение F < Fkp, то коэффициент детерминации статистически не значим (найденная оценка уравнения регрессии статистически не надежна).
Частные критерии.
Частные критерии F_x1 и F_x2 оценивают статистическую значимость включения факторов x₁ и x₂ в уравнение множественной регрессии и целесообразность включения в уравнение одного фактора после другого, т.е. F_x1 оценивает целесообразность включения в уравнение x₁ после включения в него фактора x₂.
Соответственно F_x2 указывает на целесообразность включения в модель фактора x2 после включения фактора x₁.

Поскольку фактическое значение F > Fkp, то коэффициент F_x1 статистически значим, т.е. целесообразно включать в уравнение x₁ после включения в него фактора x₂. Прирост факторной дисперсии за счет дополнительного фактора x₁ является существенным.

Поскольку фактическое значение F < Fkp, то коэффициент F_x2 статистически не значим, т.е. не целесообразно включать в уравнение x₂ после включения в него фактора x₁.

Перейти к онлайн решению своей задачи

Частные F-критерии

Правила ввода данных

Поиск

Процесс

Сообщение