Множественный коэффициент корреляции и коэффициент детерминации

Множественный коэффициент корреляции

Множественный коэффициент корреляции характеризует тесноту линейной связи между одной переменной и совокупностью других рассматриваемых переменных.
Особое значение имеет расчет множественного коэффициента корреляции результативного признака y с факторными x₁, x₂,…, x_m, формула для определения которого в общем случае имеет вид

$индекс множественной корреляции$

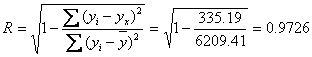
где ∑(y_i-y_x)² - необъясненная (остаточная) сумма квадратов отклонений, ∑(y_i-y)² - общая сумма квадратов отклонений.
Множественный коэффициент корреляции можно найти через корреляционные матрицы:

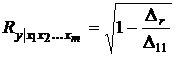
где ∆_r – определитель корреляционной матрицы; ∆₁₁ – алгебраическое дополнение элемента r_yy корреляционной матрицы.
Если рассматриваются лишь два факторных признака, то для вычисления множественного коэффициента корреляции можно использовать следующую формулу:

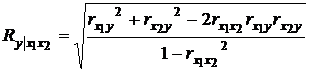
Построение множественного коэффициента корреляции целесообразно только в том случае, когда частные коэффициенты корреляции оказались значимыми, и связь между результативным признаком и факторами, включенными в модель, действительно существует.

Коэффициент детерминации

Общая формула: R² = ESS/TSS=1-RSS/TSS
где ESS - объясненная сумма квадратов отклонений, RSS - необъясненная (остаточная) сумма квадратов отклонений, TSS - общая сумма квадратов отклонений (TSS=RSS+ESS)
Сумма квадратов остатков: RSS=∑(y_i-y(x_i))²

Расчет коэффициента детерминации через определитель ,
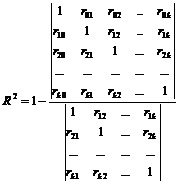где r_ij — парные коэффициенты корреляции между регрессорами xⁱ и x^j, a r_i₀ — парные коэффициенты корреляции между регрессором xⁱ и y;
— скорректированный (нормированный) коэффициент детерминации.

Квадрат множественного коэффициента корреляции R²_{y|x₁x₂...x_m}≡R² называется множественным коэффициентом детерминации; он показывает, какая доля дисперсии результативного признака y объясняется влиянием факторных признаков x₁, x₂, …,x_m. Заметим, что формула для вычисления коэффициента детерминации через соотношение остаточной и общей дисперсии результативного признака даст тот же результат.
Множественный коэффициент корреляции и коэффициент детерминации изменяются в пределах от 0 до 1. Чем ближе к 1, тем связь сильнее и, соответственно, тем точнее уравнение регрессии, построенное в дальнейшем, будет описывать зависимость y от x₁, x₂, …,x_m. Если значение множественного коэффициента корреляции невелико (меньше 0,3), это означает, что выбранный набор факторных признаков в недостаточной мере описывает вариацию результативного признака либо связь между факторными и результативной переменными является нелинейной.

Рассчитывается множественный коэффициент корреляции с помощью калькулятора. Значимость множественного коэффициента корреляции и коэффициента детерминации проверяется с помощью критерия Фишера.

Какое из приведенных чисел может быть значением коэффициента множественной детерминации:
а) 0,4;
б) -1;
в) -2,7;
г) 2,7.

Множественный линейный коэффициент корреляции равен 0.75. Какой процент вариации зависимой переменной у учтен в модели и обусловлен влиянием факторов х₁ и х₂.
а) 56,2 (R²=0.75²=0.5625);
б) 75,0;
в) 37,5

Индекс множественной корреляции

Для нелинейных моделей регрессии показатель корреляции называется индексом множественной корреляции. Для линейных моделей он равен коэффициенту множественной корреляции.
Решение осуществляем с помощью калькулятора.

1. Оценка уравнения регрессии.
Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X^TX)^-1X^TY
Матрица X

1	474.61	428.16
1	474.3	441.04
1	393.93	371.08
1	403.87	412.53
1	428.61	534.51
1	475.37	583.03
1	476.57	600.25
1	549.98	612.33
1	578.39	618.54
1	581.06	579.44

Матрица Y

130.34
126.83
108.61
116.01
135.44
142.88
158.69
168.49
174.8
187.15

Матрица X^T

1	1	1	1	1	1	1	1	1	1
474.61	474.3	393.93	403.87	428.61	475.37	476.57	549.98	578.39	581.06
428.16	441.04	371.08	412.53	534.51	583.03	600.25	612.33	618.54	579.44

Умножаем матрицы, (X^TX)

В матрице, (X^TX) число 10, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X^T и 1-го столбца матрицы X
Умножаем матрицы, (X^TY)

Находим определитель det(X^TX)^T = 14407342213.13
Находим обратную матрицу (X^TX)^-1

5.8295	-0.0116	-0.0002
-0.0116	0.0001	-0
-0.0002	-0	0

Уравнение регрессии (оценка уравнения регрессии)
Y = -32.2394 + 0.2412X ₁ + 0.1151X ₂
2. Матрица парных коэффициентов корреляции.
Число наблюдений n = 10. Число независимых переменных в модели ровно 2, а число регрессоров с учетом единичного вектора равно числу неизвестных коэффициентов. С учетом признака Y, размерность матрицы становится равным 4. Матрица, независимых переменных Х имеет размерность (10 х 4). Матрица Х^T Х определяется непосредственным умножением или по следующим предварительно вычисленным суммам.
Матрица составленная из Y и X

1	130.34	474.61	428.16
1	126.83	474.3	441.04
1	108.61	393.93	371.08
1	116.01	403.87	412.53
1	135.44	428.61	534.51
1	142.88	475.37	583.03
1	158.69	476.57	600.25
1	168.49	549.98	612.33
1	174.8	578.39	618.54
1	187.15	581.06	579.44

Транспонированная матрица.

1	1	1	1	1	1	1	1	1	1
130.34	126.83	108.61	116.01	135.44	142.88	158.69	168.49	174.8	187.15
474.61	474.3	393.93	403.87	428.61	475.37	476.57	549.98	578.39	581.06
428.16	441.04	371.08	412.53	534.51	583.03	600.25	612.33	618.54	579.44

Матрица A^TA.

10	1449.24	4836.69	5180.91
1449.24	216239.06	715766.61	770589.58
4836.69	715766.61	2379952.81	2548710.78
5180.91	770589.58	2548710.78	2764934.09

Полученная матрица имеет следующее соответствие:

∑n	∑y	∑x₁	∑x₂
∑y	∑y²	∑x₁·y	∑x₂·y
∑x₁	∑x₁·y	∑x₁²	∑x₁·x₂
∑x₂	∑x₂·y	∑x₂·x₁	∑x₂²

Найдем парные коэффициенты корреляции.
Для y и x₁
Средние значения x₁ = ∑x_i n = 4836.69 10 = 483.67 y = ∑y_i n = 1449.24 10 = 144.92 x·y = ∑x_i·y_i n = 715766.66 10 = 71576.66
Дисперсия D(x₁) = x_i² n - x² = 2379952.81 10 - 483.67² = 4059.58 D(y) = y_i² n - x² = 216239.06 10 - 144.92² = 620.94
Среднеквадратическое отклонение σ(x₁) = √ D(x₁) = √ 4059.58 = 63.71 σ(y) = √ D(y) = √ 620.94 = 24.92
Коэффициент корреляции r_x1y = x·y - x₁·y σ(x₁)·σ(y) = 71576.66-483.67·144.92 63.71·24.92 = 0.9331
Для y и x₂
Средние значения x₂ = ∑x_i n = 5180.91 10 = 518.09 x·y = ∑x_i·y_i n = 770589.58 10 = 77058.96
Дисперсия D(x₂) = x_i² n - x² = 2764934.09 10 - 518.09² = 8075.12
Среднеквадратическое отклонение σ(x₂) = √ D(x₂) = √ 8075.12 = 89.86
Коэффициент корреляции r_x2y = x·y - x₂·y σ(x₂)·σ(y) = 77058.96-518.09·144.92 89.86·24.92 = 0.8821
Для x₁ и x₂
Средние значения x₁·x₂ = ∑x_1i·x_2i n = 2548710.78 10 = 254871.08
Коэффициент корреляции r_x₁x₂ = x₁·x₂ - x₁·x₂ σ(x₁)·σ(x₂) = 254871.08-518.09·483.67 89.86·63.71 = 0.7487
Матрица парных коэффициентов корреляции.

-	y	x₁	x₂
y	1	0.93	0.88
x₁	0.93	1	0.75
x₂	0.88	0.75	1

Анализ первой строки этой матрицы позволяет произвести отбор факторных признаков, которые могут быть включены в модель множественной корреляционной зависимости. Факторные признаки, у которых r_yxi < 0.5 исключают из модели.
Коллинеарность - зависимость между факторами. В качестве критерия мультиколлинеарности может быть принято соблюдение следующих неравенств:
r(x_jy) > r(x_kx_j) ; r(x_ky) > r(x_kx_j).
Если одно из неравенств не соблюдается, то исключается тот параметр x_k или x_j, связь которого с результативным показателем Y оказывается наименее тесной.

3. Анализ параметров уравнения регрессии. Перейдем к статистическому анализу полученного уравнения регрессии: проверке значимости уравнения и его коэффициентов, исследованию абсолютных и относительных ошибок аппроксимации
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y - X*s (абсолютная ошибка аппроксимации)

-1.19
-6.11
3.11
3.34
2.76
-6.66
6.88
-2.42
-3.68
12.52

s_e² = (Y - X*s)^T(Y - X*s)
Несмещенная оценка дисперсии равна s² = 1 n-k ·s_e² = 335.1879 10-3 = 47.88
Оценка среднеквадратичного отклонения равна (Стандартная ошибка для оценки Y) σ = √ S² = √ 47.88 = 6.92
Найдем оценку ковариационной матрицы вектора k = σ(X^TX)^-1

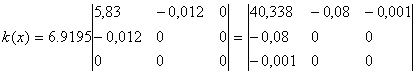
Дисперсии параметров модели определяются соотношением S²_i = K_ii, т.е. это элементы, лежащие на главной диагонали.
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле:

E₁ = 0.24· 483.67 144.92 = 0.81
Частные коэффициент эластичности E₁ < 1. Следовательно, его влияние на результативный признак Y незначительно. E₂ = 0.12· 518.09 144.92 = 0.429
Частные коэффициент эластичности E₂ < 1. Следовательно, его влияние на результативный признак Y незначительно.

Индекс множественной корреляции

$индекс множественной корреляции$
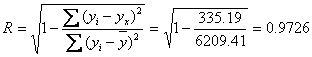
R > 0.9, связь между признаком Y факторами X сильная.
Коэффициент детерминации: R² = 0.97 ² = 0.95, т.е. в 96% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая.
Значимость коэффициента корреляции.

По таблице Стьюдента находим Tтабл:
T_табл (n-m-1;a) = (7;0.05) = 1.895
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически - значим.

4. Оценка значения результативного признака при заданных значениях факторов.
Y(0.0,0.0,) = -32.24 + 0.2412 * 0.0 + 0.1151 * 0.0 = -32.24
Доверительные интервалы с вероятностью 0.95 для индивидуального значения результативного признака.
S² = X₀^T(X^TX)^-1X₀
где X₀^T = [ 1 0.0 0.0]
(X^T·X)^-1

5.8295	-0.0116	-0.0002
-0.0116	0.0001	-0
-0.0002	-0	0

S² = 5.83 Sy = σ· √ X₀·(X^T·X)^-1·X₀ = 6.92· √ 5.83 = 16.71
(Y - t*S_Y ; Y + t*S_Y )
(-32.24 - 1.895*16.71 ; -32.24 + 1.895*16.71)
(-63.91;-0.57)
Доверительные интервалы с вероятностью 0.95 для среднего значения результативного признака. Sy = σ· √ 1+X₀·(X^T·X)^-1·X₀ = 6.92· √ 1+5.83 = 18.08
(-32.24 - 1.895*18.08 ; -32.24 + 1.895*18.08)
(-66.5;2.02)

5. Проверка гипотез относительно коэффициентов уравнения регрессии (проверка значимости параметров множественного уравнения регрессии).
1) t-статистика t_i = b_i S_{b_i} t₀ = |-32.24| 6.35 = 5.07>1.895
Статистическая значимость коэффициента регрессии b₀ подтверждается. t₁ = 0.24 0.02 = 12.2857>1.895
Статистическая значимость коэффициента регрессии b₁ подтверждается. t₂ = 0.12 0.01 = 8.2674>1.895
Статистическая значимость коэффициента регрессии b₂ подтверждается.
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b_i - t _i·S_i; b_i + t_i·S_i)
b₀: (-44.2749;-20.2039)
b₁: (0.204;0.2784)
b ₂: (0.0887;0.1415)
2) F-статистика. Критерий Фишера:
F = R² 1-R² · n-m-1 m = 40.892
Fkp = 4.35. Поскольку F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно.

Множественный коэффициент корреляции и коэффициент детерминации