Алгебраические дополнения
Определение. Если в определителе n-го порядка вычеркнуть i строку и j столбец, то оставшийся определитель (n-1)-го порядка называется минором данного элемента aij и обозначается Mij. Минором некоторого элемента определителя называется определитель, полученный из исходного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.Главным минором k-го порядка матрицы А называется определитель, составленный из элементов, расположенных на пересечении ее k строк и k столбцов с одинаковыми номерами.
Угловым минором k-го порядка матрицы А называется определитель, составленный из элементов, расположенных на пересечении ее первых k строк и первых k столбцов.
Определение. Алгебраическим дополнением элемента aij определителя D называется его минор, взятый со знаком (-1)i+j.
Алгебраическое дополнение элемента aij обозначается через Aij. Следовательно, Aij = (-1)i+jMij.
Пример №1. Дан определитель 
. Найти минор и алгебраическое дополнение элемента a21 (выделен пунктиром).
Решение. Вычеркивая в определителе первую строку и второй столбец, на пересечении которых находится элемент a21, получим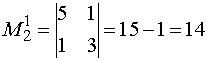 
. Тогда A21 = (-1)1+2M21 = -14.
Теорема. Определитель равен сумме произведений элементов какой-нибудь строки или столбца на их алгебраические дополнения, т.е.
D=ai01·Ai01+ai02·Ai02+ ... + ai0n·Ai0n (*)
где i0 – фиксировано.
Выражение (*) называют разложением определителя D по элементам строки с номером i0.
Вычисление определителя n-го порядка сводится к вычислению одного определителя (n-1)-го порядка, для чего в какой–либо строке (или столбце) получают (n-1) нулей, а затем разлагают определитель по этой строке, пользуясь формулой (*).
Пример №2. Покажем нахождение алгебраических дополнений на примере определения обратной матрицы:
Решение находим с помощью калькулятора. Найдем главный определитель.
∆ = 0.73 ∙(0.72 ∙0.92 -(-0.17 ∙(-0.15 )))-(-0.19 ∙(-0.07 ∙0.92 -(-0.17 ∙(-0.12 ))))+(-0.12 ∙(-0.07 ∙(-0.15 )-0.72 ∙(-0.12 ))) = 0.437197
Транспонированная матрица
Алгебраические дополнения
∆1,1 = (0.72 ∙0.92 -(-0.15 ∙(-0.17 ))) = 0.6369
∆1,2 = -(-0.07 ∙0.92 -(-0.12 ∙(-0.17 ))) = 0.0848
∆1,3 = (-0.07 ∙(-0.15 )-(-0.12 ∙0.72 )) = 0.0969
∆2,1 = -(-0.19 ∙0.92 -(-0.15 ∙(-0.12 ))) = 0.1928
∆2,2 = (0.73 ∙0.92 -(-0.12 ∙(-0.12 ))) = 0.6572
∆2,3 = -(0.73 ∙(-0.15 )-(-0.12 ∙(-0.19 ))) = 0.1323
∆3,1 = (-0.19 ∙(-0.17 )-0.72 ∙(-0.12 )) = 0.1187
∆3,2 = -(0.73 ∙(-0.17 )-(-0.07 ∙(-0.12 ))) = 0.1325
∆3,3 = (0.73 ∙0.72 -(-0.07 ∙(-0.19 ))) = 0.5123
Обратная матрица
Пример №3. Алгебраическое дополнение также используется при определении количества остовных деревьев в графе.