Системы линейных однородных уравнений
Системы линейных однородных уравнений - имеет вид ∑akixi = 0. где m > n или m < n.Однородная система линейных уравнений всегда совместна, так как rangA = rangB. Она заведомо имеет решение, состоящее из нулей, которое называется тривиальным.
Назначение сервиса. Онлайн-калькулятор предназначен для нахождения нетривиального и фундаментального решения СЛАУ. Полученное решение сохраняется в файле Word (см. пример решения).
Свойства систем линейных однородных уравнений
Для того чтобы система имела нетривиальные решения, необходимо и достаточно, чтобы ранг ее матрицы был меньше числа неизвестных.Теорема. Система в случае m=n имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.
Теорема. Любая линейная комбинация решений системы также является решением этой системы.
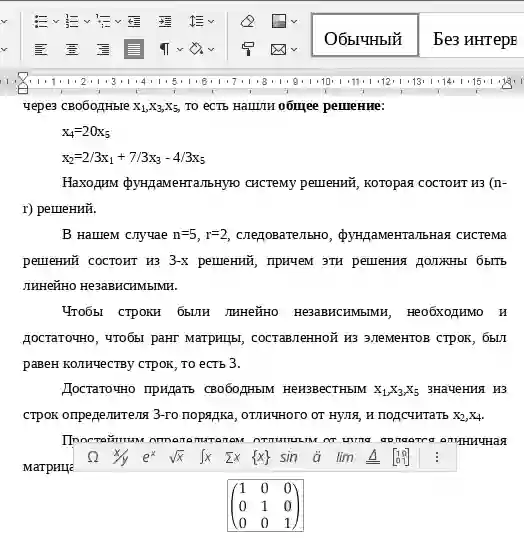
Определение. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.
Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из (n-r) решений.
Алгоритм решения систем линейных однородных уравнений
- Находим ранг матрицы.
- Выделяем базисный минор. Выделяем зависимые (базисные) и свободные неизвестные.
- Вычеркиваем те уравнения системы, коэффициенты которых не вошли в состав базисного минора, так как они являются следствиями остальных (по теореме о базисном миноре).
- Члены уравнений, содержащие свободные неизвестные, перенесем в правую часть. В результате получим систему из r уравнений с r неизвестными, эквивалентную данной, определитель которой отличен от нуля.
- Решаем полученную систему методом исключения неизвестных. Находим соотношения, выражающие зависимые переменные через свободные.
- Если ранг матрицы не равен количеству переменных, то находим фундаментальное решение системы.
- В случае rang = n имеем тривиальное решение.
Пример. Найти базис системы векторов (а1, а2,...,аm), ранг и выразить векторы по базе. Если а1=(0,0,1,-1), а2=(1,1,2,0), а3=(1,1,1,1), а4=(3,2,1,4), а5=(2,1,0,3).
Выпишем основную матрицу системы:
| 0 | 0 | 1 | -1 |
| 1 | 1 | 2 | 0 |
| 1 | 1 | 1 | 1 |
| 3 | 2 | 1 | 4 |
| 2 | 1 | 0 | 3 |
| x1 | x2 | x3 | x4 |
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 2-ую строку на (-1). Добавим 3-ую строку к 2-ой:
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 1 | 1 | 1 | 1 |
| 3 | 2 | 1 | 4 |
| 2 | 1 | 0 | 3 |
Умножим 3-ую строку на (-3). Добавим 4-ую строку к 3-ой:
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 3 | 2 | 1 | 4 |
| 2 | 1 | 0 | 3 |
Умножим 4-ую строку на (-2). Умножим 5-ую строку на (3). Добавим 5-ую строку к 4-ой:
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
Умножим 3-ую строку на (-1). Добавим 4-ую строку к 3-ой:
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 0 | 0 | 0 | 0 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы.
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
Добавим 2-ую строку к 1-ой:
| 0 | 0 | 0 | 0 |
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы.
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
Найдем ранг матрицы.
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
| x1 | x2 | x3 | x4 |
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 3.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2,x3, значит, неизвестные x1,x2,x3 – зависимые (базисные), а x4 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
| 0 | 0 | -1 | -1 |
| 0 | -1 | -2 | -1 |
| 2 | 1 | 0 | -3 |
| x1 | x2 | x3 | x4 |
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
- x3 = - x4
- x2 - 2x3 = - x4
2x1 + x2 = - 3x4
Методом исключения неизвестных находим нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x1,x2,x3 через свободные x4, то есть нашли общее решение:
x3 = x4
x2 = - x4
x1 = - x4
