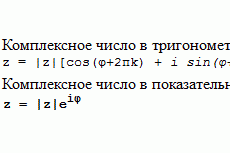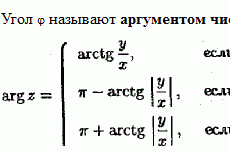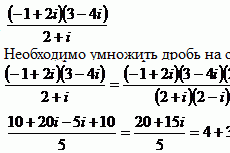Как найти нетривиальное и фундаментальное решение системы линейных однородных уравнений
Пример 1. Найти общее решение и какую-нибудь фундаментальную систему решений для системы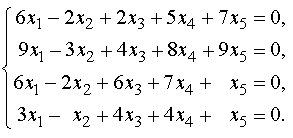
Решение находим с помощью калькулятора. Алгоритм решения такой же, как и для систем линейных неоднородных уравнений.
Оперируя только со строками, находим ранг матрицы, базисный минор; объявляем зависимые и свободные неизвестные и находим общее решение.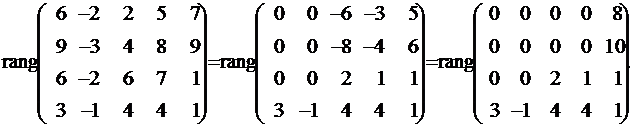
Первая и вторая строки пропорциональны, одну из них вычеркнем: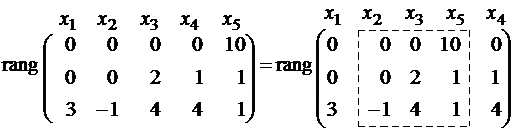
Зависимые переменные – x2, x3, x5, свободные – x1, x4. Из первого уравнения 10x5 = 0 находим x5 = 0, тогда
2x3=-x5-x4 → x3=-x4/2.
-x2=-3x1-4x3-x5-4x4 → -x2=-3x1+2x4-4x4; x2=3x1+2x4
Общее решение имеет вид:
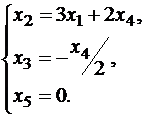
Находим фундаментальную систему решений, которая состоит из (n-r) решений. В нашем случае n=5, r=3, следовательно, фундаментальная система решений состоит из двух решений, причем эти решения должны быть линейно независимыми. Чтобы строки были линейно независимыми, необходимо и достаточно, чтобы ранг матрицы, составленной из элементов строк, был равен количеству строк, то есть 2. Достаточно придать свободным неизвестным x1 и x4 значения из строк определителя второго порядка, отличного от нуля, и подсчитать x2, x3, x5. Простейшим определителем, отличным от нуля, является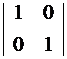
.
Таким образом, первое решение: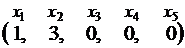
, второе – 
.
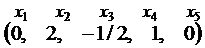Эти два решения составляют фундаментальную систему решений. Заметим, что фундаментальная система не единственна (определителей, отличных от нуля, можно составить сколько угодно).
Оперируя только со строками, находим ранг матрицы, базисный минор; объявляем зависимые и свободные неизвестные и находим общее решение.
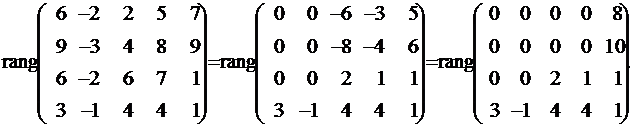
Первая и вторая строки пропорциональны, одну из них вычеркнем:
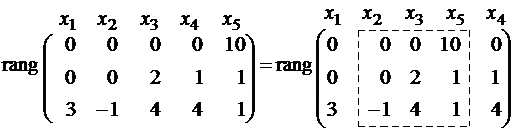
Зависимые переменные – x2, x3, x5, свободные – x1, x4. Из первого уравнения 10x5 = 0 находим x5 = 0, тогда
2x3=-x5-x4 → x3=-x4/2.
-x2=-3x1-4x3-x5-4x4 → -x2=-3x1+2x4-4x4; x2=3x1+2x4
Общее решение имеет вид:
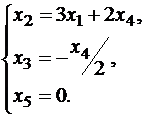
Находим фундаментальную систему решений, которая состоит из (n-r) решений. В нашем случае n=5, r=3, следовательно, фундаментальная система решений состоит из двух решений, причем эти решения должны быть линейно независимыми. Чтобы строки были линейно независимыми, необходимо и достаточно, чтобы ранг матрицы, составленной из элементов строк, был равен количеству строк, то есть 2. Достаточно придать свободным неизвестным x1 и x4 значения из строк определителя второго порядка, отличного от нуля, и подсчитать x2, x3, x5. Простейшим определителем, отличным от нуля, является
.
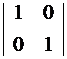Таким образом, первое решение:
, второе – .
Эти два решения составляют фундаментальную систему решений. Заметим, что фундаментальная система не единственна (определителей, отличных от нуля, можно составить сколько угодно).
Пример 2. Найти общее решение и фундаментальную систему решений системы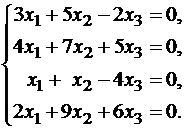 
Решение.
,
Задание. Исследовать и решить систему линейных уравнений.
Пример 4
Задание. Найти общее и частное решения каждой системы.
Решение. Выпишем основную матрицу системы:
| 5 | -2 | 9 | -4 | -1 |
| 1 | 4 | 2 | 2 | -5 |
| 6 | 2 | 11 | -2 | -6 |
| x1 | x2 | x3 | x4 | x5 |
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 2-ую строку на (-5). Добавим 2-ую строку к 1-ой:
| 0 | -22 | -1 | -14 | 24 |
| 1 | 4 | 2 | 2 | -5 |
| 6 | 2 | 11 | -2 | -6 |
Умножим 2-ую строку на (6). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
| 0 | -22 | -1 | -14 | 24 |
| 0 | 22 | 1 | 14 | -24 |
| 6 | 2 | 11 | -2 | -6 |
В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го.
| 0 | 22 | 1 | 14 | -24 |
| 6 | 2 | 11 | -2 | -6 |
Найдем ранг матрицы.
| 0 | 22 | 1 | 14 | -24 |
| 6 | 2 | 11 | -2 | -6 |
| x1 | x2 | x3 | x4 | x5 |
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 2.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2, значит, неизвестные x1,x2 – зависимые (базисные), а x3,x4,x5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
| 0 | 22 | 14 | -1 | -24 |
| 6 | 2 | -2 | -11 | -6 |
| x1 | x2 | x4 | x3 | x5 |
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
22x2 = 14x4 - x3 - 24x5
6x1 + 2x2 = - 2x4 - 11x3 - 6x5
Методом исключения неизвестных находим нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x1,x2 через свободные x3,x4,x5, то есть нашли общее решение:
x2 = 0.64x4 - 0.0455x3 - 1.09x5
x1 = - 0.55x4 - 1.82x3 - 0.64x5
Находим фундаментальную систему решений, которая состоит из (n-r) решений.
В нашем случае n=5, r=2, следовательно, фундаментальная система решений состоит из 3-х решений, причем эти решения должны быть линейно независимыми.
Чтобы строки были линейно независимыми, необходимо и достаточно, чтобы ранг матрицы, составленной из элементов строк, был равен количеству строк, то есть 3.
Достаточно придать свободным неизвестным x3,x4,x5 значения из строк определителя 3-го порядка, отличного от нуля, и подсчитать x1,x2.
Простейшим определителем, отличным от нуля, является единичная матрица.
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Задача. Найти фундаментальный набор решений однородной системы линейных уравнений. Решение
Задача. Найти общее решение системы. Проанализировать его структуру (указать базис пространства решений однородной системы, установить размерность пространства). Решение
Пример 3
Пример 4
