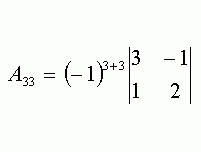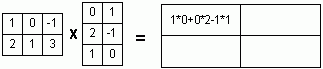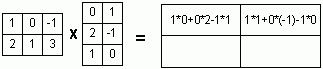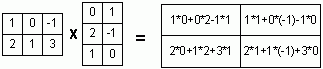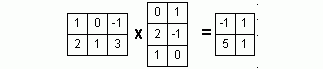Теорема Кронекера-Капелли
Теорема Кронекера-Капелли — критерий совместности системы линейных алгебраических уравнений.Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём:
- система имеет единственное решение, если ранг равен числу неизвестных;
- бесконечное множество решений, если ранг меньше числа неизвестных.
Совместная система линейных уравнений имеет единственное решение, если ранг этой системы равен количеству переменных.
Совместная система линейных уравнений имеет бесконечное множество решений, если ранг этой системы меньше количества переменных.
Пример №1. Исследовать систему алгебраических уравнений (без непосредственного решения системы) с помощью теоремы Кронекера-Капелли.
Запишем систему в виде:
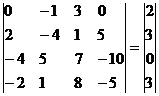
Для удобства вычислений поменяем строки местами:
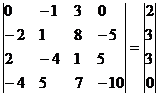
Добавим 2-ую строку к 1-ой:
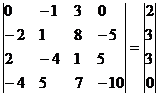
Добавим 3-ую строку к 2-ой:
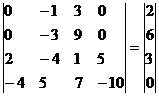
Умножим 3-ую строку на (2). Добавим 4-ую строку к 3-ой:
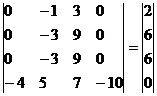
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
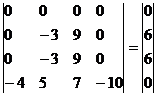
Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
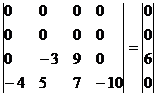
Добавим 2-ую строку к 1-ой:
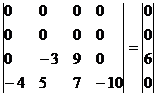
Это соответствует системе:
-3x2 + 9x3 = 6
-4x1 + 5x2 + 7x3 - 10x4 = 0
За базисные переменные примем x1 и x2. Тогда свободные x3,x4.
Ранг основной матрицы равен 2. Ранг расширенной матрицы тоже равен 2. Система совместна и имеет бесконечное множество решений.
Пример №2.
Запишем систему в виде:
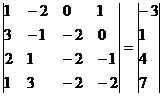
Для удобства вычислений поменяем строки местами:
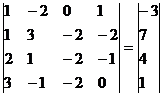
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
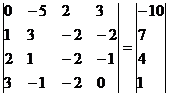
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
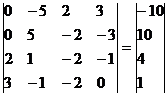
Умножим 3-ую строку на (3). Умножим 4-ую строку на (-2). Добавим 4-ую строку к 3-ой:
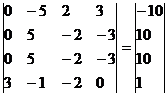
Добавим 2-ую строку к 1-ой:
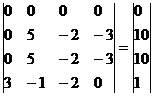
Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
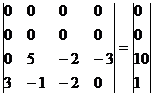
Добавим 2-ую строку к 1-ой:
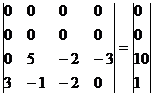
3x2 -2x3 – 3x4 = 10
3x1 -x2 -2x3 = 1
Необходимо переменные x3,x4 принять в качестве свободных переменных и через них выразить базисные – x1, x2.
Ранг основной матрицы равен 2. Ранг расширенной матрицы тоже равен 2. Система совместна и имеет бесконечное множество решений.
Пример №3. Дана система линейных уравнений у которой число уравнений равно числу неизвестных. При каком условии эта система имеет единственное решение?
Ответ: Система имеет единственное решение, если ранг этой системы будет равен количеству переменных.
