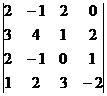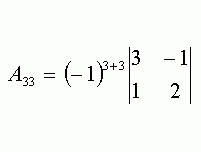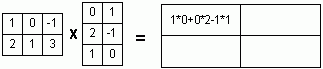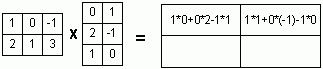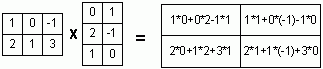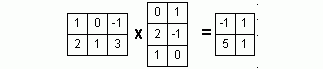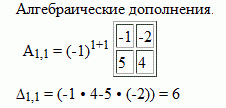Применение методов Гаусса и Жордано-Гаусса
- Решение системы уравнений методом Жордано-Гаусса
Система линейных уравнений:
2x1 + x2 - x3 + 3x4 - 2x5 = 2
x1 - x2 + x4 = 0
x1 - x3 + x4 - 2x5 = -1 - Пример нахождения обратной матрицы методом Жордано-Гаусса
- Теорема Кронекера-Капелли
- Общее решение однородной СЛАУ
- Метод Гаусса в Excel
Применение формул Крамера
- Пример решения СЛАУ методом Крамера
- Как найти определитель методом понижения порядка
- Метод Крамера в Excel
Применение метода обратной матрицы
- Пример нахождения обратной матрицы
- Пример нахождения присоединённой матрицы
- Пример нахождения алгебраических дополнений.
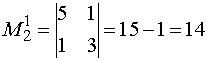
- Как найти координаты вектора в базисе
Доказать, что векторы a, b, c образуют базис, и найти координаты вектора d в этом базисе. - Вычисление обратной матрицы в Excel
Примеры с матрицами
Вычислить АВ – ВА, если:А
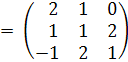 , В =
, В = 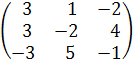 .
.
Решаем с помощью сервиса умножения матриц. Указываем размерность 3x3.
Решение в Excel
Найти обратную матрицу для матрицы А и сделать проверку, если:
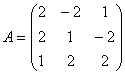
Решение в Excel
Скачать решение
Вычисление определителей
Вычислить определители:а) второго порядка
Скачать решение
б) третьего порядка двумя способами:
1) правилом треугольников,
Скачать решение
2) разложением по элементам любой строки (столбца),
Перейти к онлайн решению своей задачи
Решение систем алгебраических уравнений
Решить систему алгебраических уравнений тремя методами (методом Крамера, методом обратной матрицы и методом Жордана-Гаусса):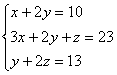
Скачать решение методом Крамера
Скачать решение методом Гаусса
Скачать решение методом обратной матрицы
Векторное пространство
Найти линейную комбинацию 2а1 - 3а2 + а3 следующих векторов:а1=(1; 0; 3; -2),
а2 =(-1; 1; 4; 3),
а3 =(-5; 3; 5; 3).
Даны четыре вектора а =(4; 5; 2), b =(3; 0; 1), c =(-1; 4; 2), d =(5; 7; 8) в некотором базисе. Показать, что векторы a, b, c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Используя онлайн-калькулятор, проверяем на равенство нулю определителя. Векторы образуют базис трехмерного пространства, если определитель системы не равен 0. Далее используем либо метод Крамера, либо метод матриц.
Скачать решение
Пример контрольной работы по математике
Примечание. Все ссылки, указанные в данной статье, ведут на соответствующие онлайн-калькуляторы.Решите систему линейных уравнений
а) методом Крамера;
б) с помощью обратной матрицы
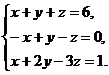
3. Задание: найдите AB, BA, AC, AT ,|A|, αA, где «α» - порядковый номер по журналу
A=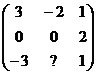 ; B=
; B=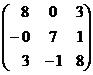 ; C=
; C=![]() ;α=2.
;α=2.
Примечание: Умножение матриц производится через онлайн-калькулятор.
4. Для производства продукции пяти видов в количестве 20, 30, 28, ?, 56 соответственно предприятие тратит сырье в количестве 2, 3, 4, 2, 3 кг. на ед. продукции соответственно.
Составить вектор объема производства и затрат сырья на ед. продукции, определить общие затраты сырья, определите стоимость сырья на производство продукции, если 1 кг сырья стоит 25 руб, где «?» - порядковый номер журнала
Решение:
Вектор объема производства: 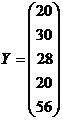
Вектор затрат сырья на ед. продукции: s = (2;3;4;2;3)
Общие затраты сырья:
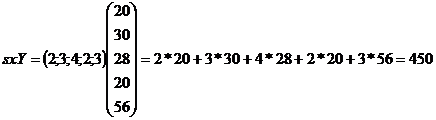
Стоимость сырья на производство продукции: 450 кг. х 25 руб./кг = 11250 руб.
6. Найти ранг матрицы A = 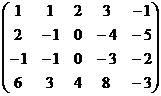
7. Исследовать на совместность, найти общее решение и одно частное решение системы уравнений 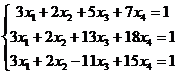
Вывод: онлайн-калькуляторы охватывают большую часть разделов высшей математики. С ними легко можно решать любые контрольные работы по линейной алгебре.