Базисные решения системы линейных уравнений методом Жордана-Гаусса
Назначение сервиса. С помощью данного онлайн-калькулятора находятся базисные решения системы линейных уравнений, определяется опорное решение. Полученное решение сохраняется в файле Word.При решении используется метод прямоугольника, в результате применения которого получается диагональная матрица — квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.
Система линейных уравнений:
2x1 + x2 - x3 + 3x4 - 2x5 = 2
x1 - x2 + x4 = 0
x1 - x3 + x4 - 2x5 = -1
Запишем ее через матрицу.
| 2 | 1 | -1 | 3 | -2 |
| 1 | -1 | 0 | 1 | 0 |
| 1 | 0 | -1 | 1 | -2 |
Решение системы линейных уравнений называется базисным, если свободные переменные (m>n) обращаются в ноль.
Пример №1. Найти три базисных решения системы линейных уравнений методом Жордана-Гаусса, указать среди них опорные.
Решение. Запишем систему в виде:
| 2 | 1 | -1 | 3 | -2 | 2 |
| 1 | -1 | 0 | 1 | 0 | 0 |
| 1 | 0 | -1 | 1 | -2 | -1 |
Разрешающий элемент равен (2).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
РЭ - разрешающий элемент (2), А и В - элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | x4 | x5 | B |
| 2 / 2 = 1 | 1 / 2 = 0.5 | -1 / 2 = -0.5 | 3 / 2 = 1.5 | -2 / 2 = -1 | 2 / 2 = 1 |
| 1 | 0.5 | -0.5 | 1.5 | -1 | 1 |
| 0 | -1.5 | 0.5 | -0.5 | 1 | -1 |
| 0 | -0.5 | -0.5 | -0.5 | -1 | -2 |
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | x4 | x5 | B |
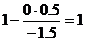
| 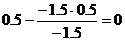
| 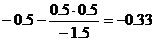
| 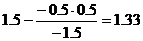
| 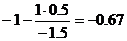
| 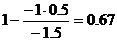
|
| 0 / -1.5 = 0 | -1.5 / -1.5 = 1 | 0.5 / -1.5 = -0.33 | -0.5 / -1.5 = 0.33 | 1 / -1.5 = -0.67 | -1 / -1.5 = 0.67 |
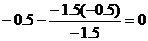
| 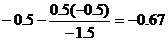
| 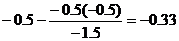
| 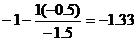
| 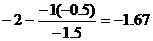
|
| 1 | 0 | -0.33 | 1.33 | -0.67 | 0.67 |
| 0 | 1 | -0.33 | 0.33 | -0.67 | 0.67 |
| 0 | 0 | -0.67 | -0.33 | -1.33 | -1.67 |
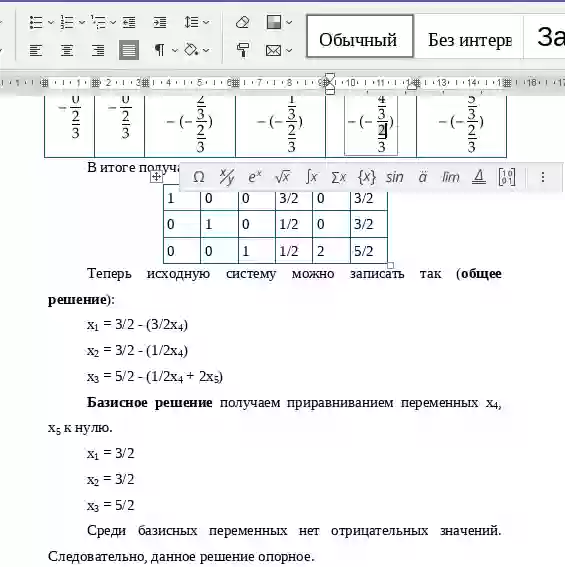
Разрешающий элемент равен (-0.67). После пересчета получим общее решение системы:
x1 = 1.5 - 1.5x4
x2 = 1.5 - 0.5x4
x3 = 2.5 - 0.5x4 + 2x5
Необходимо переменные x4,x5 принять в качестве свободных переменных и через них выразить базисные.
Приравняем переменные x4 и x5 к 0. Получим базисное решение системы.
x1 = 1.5, x2 = 1.5, x3 = 2.5
Поскольку среди базисного решения нет отрицательных значений, то полученное решение является опорным.
Для получения частного решения, необходимо задать любые значения x4 и x5. Пусть x4=1 и x5=1.
x1 = 0, x2 = 1, x3 = 4
Пример №2. Используя метод Жордана-Гаусса, привести систему к единичному базису. Найти одно из: а) базисных решений, б) опорных решений системы.
Запишем систему в виде:
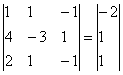
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
РЭ - разрешающий элемент (1), А и В - элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | B |
| 1 / 1 = 1 | 1 / 1 = 1 | -1 / 1 = -1 | -2 / 1 = -2 |
| | | | |
| |
| |
|
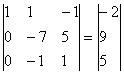
Разрешающий элемент равен (-7).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | B |
| |
| |
|
| 0 / -7 = 0 | -7 / -7 = 1 | 5 / -7 = -0.71 | 9 / -7 = -1.29 |
| |
| |
|
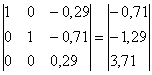
Разрешающий элемент равен (0.29).
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | B |
| |
| |
|
| | | | |
| 0 / 0.29 = 0 | 0 / 0.29 = 0 | 0.29 / 0.29 = 1 | 3.71 / 0.29 = 13 |
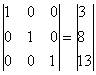
x1 = 3, x2 = 8, x3 = 13