Правило прямоугольника
Правило прямоугольника применяется в методе Жордана-Гаусса.Алгоритм пересчета таблиц по правилу прямоугольника.
Выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Назначение сервиса. Онлайн-калькулятор Правило прямоугольника предназначен для пересчета таблиц методом жордановских преобразований.
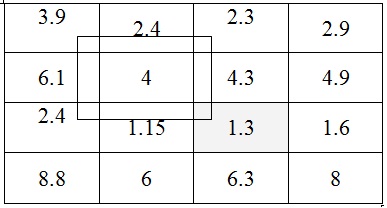
Примечание. Данный метод не стоит путать с формулой прямоугольников.
Пример №1. Производится пересчет элементов новой симплекс-таблицы. Каким будет значение элемента x25 в новой симплекс-таблице, если до пересчета x25 = -3 , x27 =5 , х45 = -8 , х47 =2
Решение.
x25 =x25 - x45*x27/x47 = -3 - (-8)*5/2 = -3+20 = 17
Пример №2. По приведенной ниже симплекс-таблице определите, является ли соответствующее ей базисное решение оптимальным. Если решение не является оптимальным, осуществите пересчет таблицы.
| ПЧ | X3 | X4 | |
| F | -5 | 2 | -1 |
| X1 | 4 | 2 | 1 |
| X2 | 3 | 1 | 2 |
Решение.
Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных xj≥0, что эквивалентно условию неотрицательности bj≥0.
Поскольку X1 = 4 > 0, X2 = 3 > 0, то это допустимое базисное решение. Определим, является ли оно оптимальным. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный, и его необходимо улучшить. В индексной строке X4 = -1 < 0, поэтому план не является оптимальным. Осуществим пересчет таблицы.
Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее: min (4:1 , 3:2 ) = 11/2
Следовательно, 2-ая строка является ведущей. Вместо переменной x4 в план войдет переменная x2.
Таблица 1
| ПЧ | X3 | X4 | |
| F | -5 | 2 | -1 |
| X1 | 4 | 2 | 1 |
| X2 | 3 | 1 | 2 |
Разрешающий элемент РЭ=2. Строка, соответствующая переменной x2 , получена в результате деления всех элементов строки x на разрешающий элемент РЭ=2 (см. табл.2) . На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Все остальные элементы, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
СТЭ - элемент старого плана, РЭ - разрешающий элемент (2), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ (см. табл.2).
Формируем таблицу.
Таблица 2
| 4-(3 • 1):2 | 2-(1 • 1):2 | 1-(2 • 1):2 |
| 3 : 2 | 1 : 2 | 2 : 2 |
| -5-(3 • -1):2 | 2-(1 • -1):2 | -1-(2 • -1):2 |
Получаем новую таблицу:
Таблица 3
| ПЧ | X3 | X2 | |
| F | -31/2 | 21/2 | 0 |
| X1 | 21/2 | 11/2 | 0 |
| X4 | 11/2 | 1/2 | 1 |
Поскольку X3≥0, X2≥0, то получили оптимальный план.
Пример №3. Решить задачу линейного программирования симплекс-методом, используя в качестве начальной угловой точки:
f(x) = -2x1 + x2 + 4x3 – x4 – x5 → min
x2 + 2x4 – x5 = 1
x1 - x4 – x5 = 1
2x2 + x3 + 2x5 = 4
xj ≥ 0, j=1,..,5, x0 = (1;1;2;0;0)
Решение.
Сведем задачу F(X) → min к задаче F(X) → max. Для этого умножаем F(X) на (-1).
0x1-1x2 + 0x3-2x4 + 1x5 = -1
-1x1 + 0x2 + 0x3 + 1x4 + 1x5 = -1
0x1-2x2-1x3 + 0x4-2x5 = -4
F(x) = 2x1 - x2 - 4x3 + x4 + x5
Затем систему ограничений преобразуем методом Гаусса-Жордана к такой форме, чтобы базисными стали переменные x1, x2, x3, а вектор b = (1, 1, 2)T
|
-1 |
0 | -1 | 0 | -2 | 1 |
| -1 | -1 | 0 | 0 | 1 | 1 |
| -4 | 0 | -2 | -1 | 0 | -2 |
| 0 | -2 | 1 | 4 | -1 | -1 |
Итерация №1. Разрешающий элемент РЭ=-1.
Формируем таблицу.
Строка, соответствующая переменной x2 , получена в результате деления всех элементов строки x2 на разрешающий элемент РЭ=-1. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Все остальные элементы, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую таблицу:
| -1 | 0 | -1 | 0 | -2 | 1 |
| 1 | 1 | 0 | 0 | -1 | -1 |
| -4 | 0 | -2 | -1 | 0 | -2 |
| 2 | 0 | 1 | 4 | -3 | -3 |
Итерация №2. Разрешающий элемент РЭ=-1.
Строка, соответствующая переменной x4, получена в результате деления всех элементов строки x3 на разрешающий элемент РЭ=-1. На месте разрешающего элемента получаем 1. В остальных клетках столбца x4 записываем нули.
Все остальные элементы, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую таблицу:
| -1 | 0 | -1 | 0 | -2 | 1 |
| 1 | 1 | 0 | 0 | -1 | -1 |
| 4 | 0 | 2 | 1 | 0 | 2 |
| -14 | 0 | -7 | 0 | -3 | -11 |
Итерация №3. Разрешающий элемент РЭ=-1. Строка, соответствующая переменной x3 , получена в результате деления всех элементов строки x1 на разрешающий элемент РЭ=-1. На месте разрешающего элемента получаем 1. В остальных клетках столбца x3 записываем нули. Все остальные элементы, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую таблицу:
| 1 | 0 | 1 | 0 | 2 | -1 |
| 1 | 1 | 0 | 0 | -1 | -1 |
| 2 | 0 | 0 | 1 | -4 | 4 |
| -7 | 0 | 0 | 0 | 11 | -18 |
Далее необходимо переназначить переменные и решать симплекс-методом.
