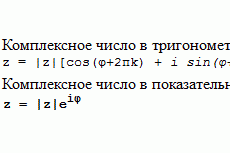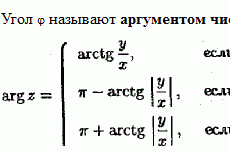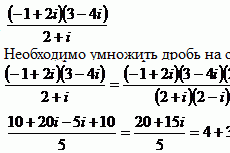Методы оптимизации
Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом).Методы оптимизации классифицируют в соответствии с задачами оптимизации:
- Локальные методы: сходятся к локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.
- Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.
- Детерминированные;
- Случайные (стохастические);
- Комбинированные.
- Методы одномерной оптимизации ;
- Методы многомерной оптимизации.
Термины и определения
Градиент функции f(x1,x2,…,xn) определяется как вектор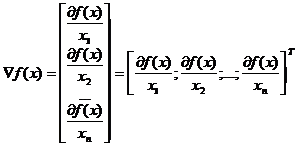
Матрица, составленная из вторых производных функции, называется матрицей Гессе. Матрица Гессе (гессиан) для функции f(x1,…,xn) есть симметрическая матрица порядка nxn:
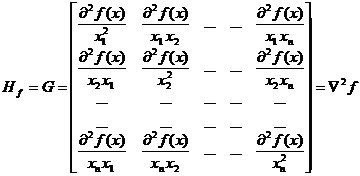
Норма вектора (норма матрицы), S(x1,x2)
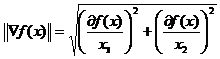
Онлайн калькуляторы по методам оптимизации
В данном разделе представлены онлайн сервисы следующих направлений.Функция одной переменной
- Наибольшее и наименьшее значение функции одной переменной.
- Интервалы выпуклости и вогнутости функции.
- Полное исследование функции.
Методы поиска нулей функции
- Метод Ньютона (Метод касательных), Метод половинного деления (метод дихотомии)
- Метод хорд
- Комбинированный метод
- Метод итераций
- Метод секущих
Методы минимизации функций
Функция одной переменной
- Метод Свенна
- Одномерный поиск
- Метод Ньютона
- Метод деления отрезка пополам
- Метод Фибоначчи
- Метод золотого сечения
- Метод Пауэлла
- Интервалы возрастания и убывания функции. Точки перегиба (интервалы выпуклости и вогнутости).
Функция двух переменных
- Матрица Гессе.
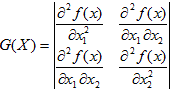 . Позволяет ответить на вопрос является ли функция выпуклой или вогнутой, а также определить тип экстремума (минимум или максимум).
. Позволяет ответить на вопрос является ли функция выпуклой или вогнутой, а также определить тип экстремума (минимум или максимум).
- Градиент функции. Вычисление градиента в точке A, нахождение производной в точке A по направлению вектора a .
- Производные второго порядка
- Экстремум функции двух переменных.
Методы прямого поиска
- Метод Хука–Дживса
- Метод сопряженных направлений (метод Пауэлла). Найти минимум целевой функции методом сопряженных направлений: f(x)=3x1 – x13 + 3x22 + 4x2. x0=(0.78;1)
Градиентные методы
- Метод наискорейшего спуска (метод Коши).
- Метод Ньютона, модифицированный метод Ньютона.
- Метод Марквардта. Найти минимум функции: y=x12+4x22+x1x2+1-5x2 методом Марквардта с начальной точкой (10;10) и εx=εy= ε|▽f(x)|=0.5. Предельное число итераций равно M=5.
- Метод сопряженных градиентов (метод Флетчера-Ривса, метод Миля-Кентрелла, метод Поллака-Рибьера)
- Метод Бройдена–Флетчера–Гольдфарба–Шанно (квазиньютоновские методы).
Линейное программирование
- Графический метод решения задач линейного программирования.
- Задача линейного программирования сводится к приведению к канонической форме, а затем к стандартной форме ЗЛП.
- Симплекс-метод.
- Двойственный симплекс-метод (P-метод).
- Составление и решение двойственной задачи.
- Метод Гомори.
- Задачи параметрического программирования.
Нелинейное программирование
Прямые методы
- Метод множителей Лагранжа. В задачах 301-320 используя метод множителей Лагранжа найти точки экстремума функции
z=f(x,y)при заданном условии:z=xy+7x,2x+y=1 - Условия Куна-Таккера.
Градиентные методы
Методы линеаризации для задач условной оптимизации
- Метод непосредственной линеаризации.
- Алгоритм Франка-Вульфа.
- Метод допустимых направлений Зойтендейка.
Итерационные методы решения СЛАУ
Прямые методы решения СЛАУ
Численное интегрирование функций
Вычисление определителей
- Вычисление определителя матрицы методом декомпозиции
- Нахождение определителя правилом Саррюса.
- Определитель методом Гаусса.
- Расчет определителя через алгебраические дополнения.