Поиск минимума методом Ньютона
В основе поиска минимума функции методом Ньютона лежит алгоритм метода Ньютона нахождения корней функции. При этом исходная функция f(x) заменяется на ее первую производную. Чтобы найти минимум функции двух переменных методом Ньютона, используйте этот калькулятор.- 10•x•e2x =
10*x*exp(2*x) - x•e-x+cos(3x) =
x*exp(-x)+cos(3*x) - x3-x2+3 =
x^3-x^2+3
Метод Ньютона применим для вогнутой (или выпуклой) функции F(x), что соответствует монотонности ее первой производной f(x).
Известно, что если функция F(x) имеет локальный минимум (или максимум) в точке X0, то в этой точке градиент функции F(x) (вектор ее производных) равен нулю, т.е. F’(x) ≡ f(x)=0.
Следовательно, если функция F(x) дифференцируема, то для нахождения ее экстремума нужно решить уравнение f(x)=0
где f(x) = F’(x). x - корень уравнения, точка, то есть, координата в которой F'(x)=0 (рис.1).
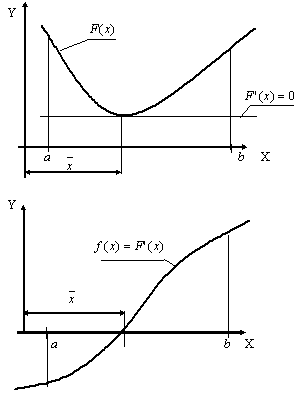
Рис. 1.Вогнутая функция F(x) и ее производная f(x).
Алгоритм метода Ньютона сводится к линейному представлению функции f(x) и решению уравнения. Точка экстремума равна:
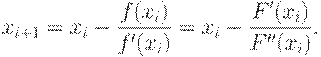
Словесный алгоритм метода Ньютона
- Если F’(a)F’’’(a)>0,то x=a, иначе x=b.
- Находим приближение корня xi+1.
- Продолжаем итерационный процесс до тех пор, пока |f’(x0)|<ε
В точке экстремума x производная F’(x) меняет знак.
Если в точке x0 функция F(x) имеет минимум, то производная F’(x) в окрестности x меняет знак с отрицательного на положительный, т.е. F’(x) является возрастающей функцией, значит,
F’’(x)>0 (рис. 2 a).
Если в точке x0 функция F(x) имеет максимум, то производная F’(x) в окрестности x меняет знак с положительного на отрицательный, т.е. F’(x) является убывающей функцией, значит,
F’’(x)<0 (рис. 2 b).
Следовательно, по знаку F’’(x) можно судить: в точке x максимум или минимум функции F(x).
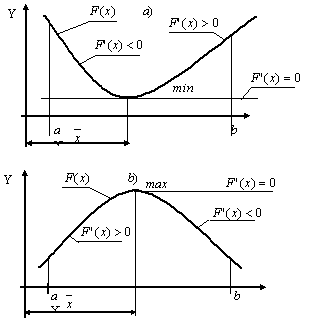
Рис. 2.
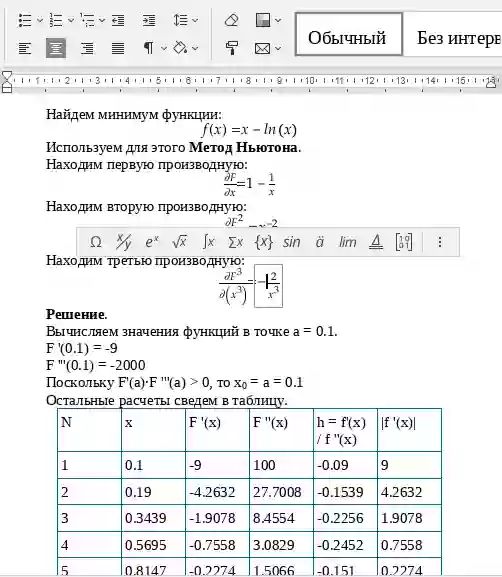
Пример. Найти минимальное значение f(x)=x-ln(x), [0.1;2] методом касательных, используя в качестве условия достижения требуемой точности неравенство |f’(xn)|≤0,01.
Решение. Используем для этого Метод Ньютона. Находим первую производную: dF/dx = 1-1/x. Находим вторую производную: d2F/dx2 = x-2. Находим третью производную: d3F/dx3 = -2/x3
Вычисляем значения функций в точке a = 0.1, F'(0.1) = -9
F'''(0.1) = -2000
Поскольку F'(a)•F'''(a) > 0, то x0 = a = 0.1. Остальные расчеты сведем в таблицу.
| N | x | F'(x) | F''(x) | h = f'(x) / f''(x) | |f'(x)| |
| 1 | 0.1 | -9 | 100 | -0.09 | 9 |
| 2 | 0.19 | -4.2632 | 27.7008 | -0.1539 | 4.2632 |
| 3 | 0.3439 | -1.9078 | 8.4554 | -0.2256 | 1.9078 |
| 4 | 0.5695 | -0.7558 | 3.0829 | -0.2452 | 0.7558 |
| 5 | 0.8147 | -0.2274 | 1.5066 | -0.151 | 0.2274 |
| 6 | 0.9657 | -0.03556 | 1.0724 | -0.03316 | 0.03556 |
| 7 | 0.9988 | -0.00118 | 1.0024 | -0.00118 | 0.00118 |
Ответ: x = 0.9988 - (-0.00118) / 1.0024 = 0.99999860; F(x) = 1
Параметр сходимости. Скорость сходимости метода Ньютона квадратичная с коэффициентом α = M2/2m1, где M2 = max|f "(x)|, m1 = min|f'(x)|.