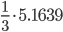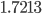Формула Симпсона
Остаточный член квадратурной формулы Симпсона равен
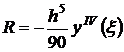 , где ξ∈(x0,x2) или
, где ξ∈(x0,x2) или 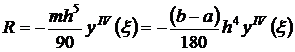
Назначение сервиса. Сервис предназначен для вычисления определенного интеграла по формуле Симпсона в онлайн режиме.
Инструкция. Введите подынтегральную функцию f(x), нажмите Решить. Полученное решение сохраняется в файле Word. Также создается шаблон решения в Excel.
Правила ввода функции
1)
10•x•e2x ≡ 10*x*exp(2*x)
2)
x•e-x+cos(3x) ≡ x*exp(-x)+cos(3*x)
3)
x3-x2+3 ≡ x^3-x^2+3
Вывод формулы Симпсона
Из формулы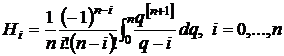
при n = 2 получаем
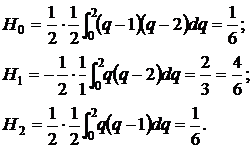
Т.к. x2-x0 = 2h, то имеем
Это формула Симпсона. Геометрически это означает, что кривую y=f(x) мы заменяем параболой y=L2(x), проходящей через три точки: M0(x0,y0), M1(x1,y1), M2(x2,y2).

Остаточный член формулы Симпсона равен
Предположим, что y∈C(4)[a,b]. Получим явное выражение для R. Фиксируя среднюю точку x1 и рассматривая R=R(h) как функцию h, будем иметь:
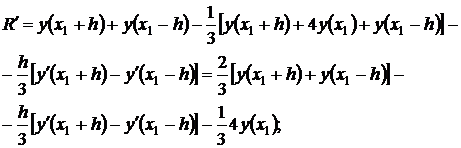
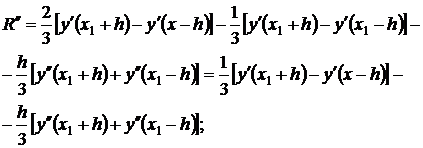
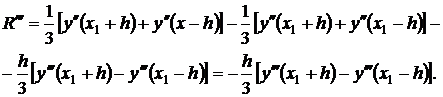
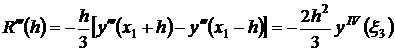
где ξ3∈(x1-h,x1+h). Кроме того, имеем: R(0) = 0, R'(0)=0. R''(0)=0. Теперь, последовательно интегрируя R'''(h), используя теорему о среднем, получим
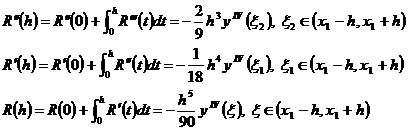
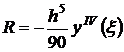 , где ξ∈(x0,x2). (11)
, где ξ∈(x0,x2). (11)
Следовательно, формула Симпсона является точной для полиномов не только второй, но и третьей степени.
Получим теперь формулу Симпсона для произвольного интервала [a,b]. Пусть n = 2m есть четное число узлов сетки {xi}, xi=a+i·h, i=0,...,n,
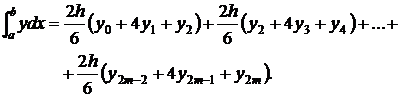
Отсюда получаем общую формулу Симпсона
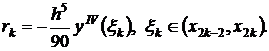
Т.к. число удвоенных промежутков равно m, то
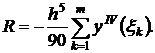
С учетом непрерывности yIV на [a,b], можно найти точку ε, такую, что
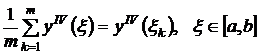 .
.
Поэтому будем иметь
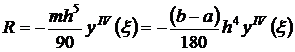 . (13)
. (13)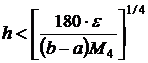 .
.
На практике вычисление R по формуле (13) бывает затруднительным. В этом случае можно поступить следующим образом. Вычисляем интеграл I(h)=I1 с шагом h, I(2h)=I2 с шагом 2h и т.д. и вычисляем погрешность Δ:
Δ = |Ik-Ik-1| ≤ ε. (14)
Если неравенство (14) выполняется (ε - заданная погрешность), то за оценку интеграла берут Ik = I(k·h).
Замечание. Если сетка неравномерная, то формула Симпсона приобретает следующий вид:
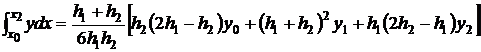
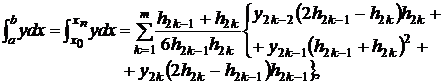
Пример №1. С помощью формулы Симпсона вычислить интеграл ![]() , приняв n = 10.
, приняв n = 10.
Решение: Имеем 2m = 10. Отсюда ![]() . Результаты вычислений даны в таблице:
. Результаты вычислений даны в таблице:
| i | xi | y2i-1 | y2i |
| 0 | 0 | y0= 1.00000 | |
| 1 | 0.1 | 0.90909 | |
| 2 | 0.2 | 0.83333 | |
| 3 | 0.3 | 0.76923 | |
| 4 | 0.4 | 0.71429 | |
| 5 | 0.5 | 0.66667 | |
| 6 | 0.6 | 0.62500 | |
| 7 | 0.7 | 0.58824 | |
| 8 | 0.8 | 0.55556 | |
| 9 | 0.9 | 0.52632 | |
| 10 | 1.0 | yn=0.50000 | |
| ∑ | σ1 | σ2 | |
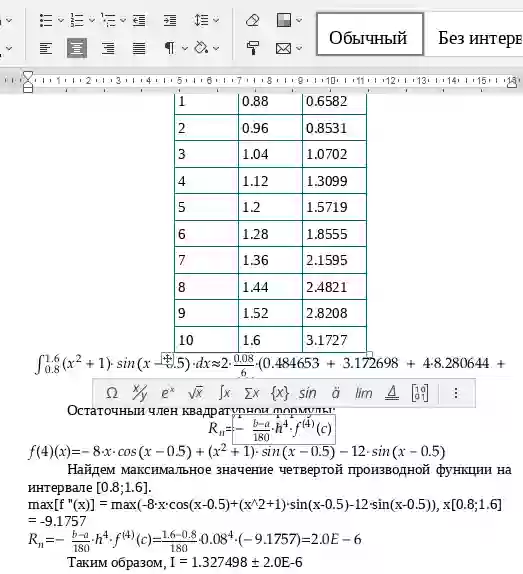
По формуле (12) получим
Рассчитаем погрешность R=R2. Т.к.
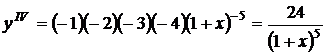 .
.
Отсюда max|yIV|=24 при 0≤x≤1 и, следовательно
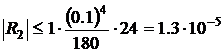 . Таким образом, I = 0.69315 ± 0.00001.
. Таким образом, I = 0.69315 ± 0.00001.
Пример №2. В задачах вычислить определенный интеграл приближенно по формуле Симпсона, разбив отрезок интегрирования на 10 равных частей. Вычисления производить с округлением до четвертого десятичного знака.
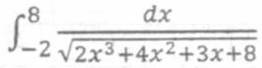
Решение:
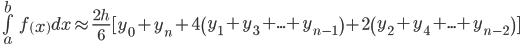
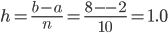
| i | xi | yi |
| 0 | -2 | 0.7071 |
| 1 | -1 | 0.378 |
| 2 | 0 | 0.3536 |
| 3 | 1 | 0.2425 |
| 4 | 2 | 0.1474 |
| 5 | 3 | 0.09667 |
| 6 | 4 | 0.06868 |
| 7 | 5 | 0.05178 |
| 8 | 6 | 0.04076 |
| 9 | 7 | 0.03313 |
| 10 | 8 | 0.02761 |
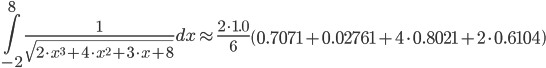 =
=