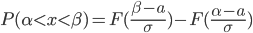Метод хорд
Назначение сервиса. Сервис предназначен для нахождения корней уравненийf(x) в онлайн режиме методом хорд.
F(x), нажмите Далее. Полученное решение сохраняется в файле Word. Также создается шаблон решения в Excel. Ниже представлена видеоинструкция.
Правила ввода функции
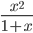 ≡ x^2/(1+x)
≡ x^2/(1+x)
cos2(2x+π) ≡ (cos(2*x+pi))^2
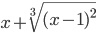 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)
f’’(x)>0 f’’(x)<0
f(b)f’’(b)>0 f(a)f’’(a)>0
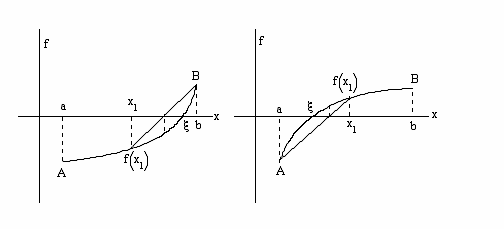
Рассмотрим рис.1а. Проведем через точки А и В хорду. Уравнение хорды
![]() .
.
В точке x=x1, y=0, в результате получим первое приближение корня
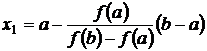 . (3.8)
. (3.8)
Проверяем условия
(а) f(x1)f(b)<0,
(б) f(x1)f(a)<0.
Если выполняется условие (а), то в формуле (3.8) точку a заменяем на x1, получим
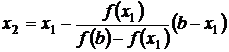 .
.Продолжая этот процесс, получим для n-го приближения
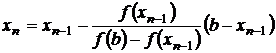 . (3.9)
. (3.9)
Здесь подвижен конец a, то есть f(xi)f(b)<0. Аналогичная ситуация на рис 2а.
Рассмотрим случай, когда неподвижен конец a.
f’’(x)<0 f’’(x)>0
f(b)f’’(b)<0 f(a)f’’(a)<0
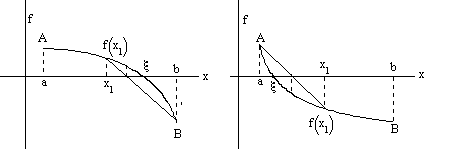
На рис 1б,2б выполняется f(xi)f(a)<0. Записав уравнение хорды, мы на первом шаге итерационного процесса получим x1 (см. (3.8)). Здесь выполняется f(x1)f(a)<0. Затем вводим b1=x1 (в формуле (3.8) точку b заменяем на x1), получим
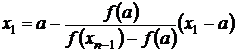 .
.
Продолжая процесс, придем к формуле
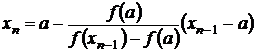 . (3.10)
. (3.10)
Останов процесса
|xn – xn-1|<ε; ξ≈xn
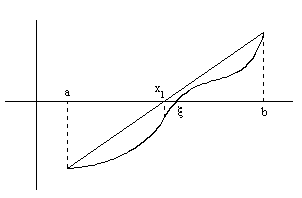
Рис. 3
На рис.3 f’’(x) меняет знак, поэтому подвижными будут оба конца.
Прежде чем перейти к вопросу о сходимости итерационного процесса метода хорд введем понятие выпуклой функции.
Определение. Непрерывная на [a,b] функция называется выпуклой (вогнутой), если для любых двух точек x1,x2, удовлетворяющих a≤x1<x2≤b и aÎ[0,1] выполняется соотношение
f(αx1 + (1-α)x2) ≤ αf(x1) + (1-α)f(x2) - выпуклая.
f(αx1 + (1-α)x2) ≥ αf(x1) + (1-α)f(x2) - вогнутая
Для выпуклой функции f’’(x)≥0.
Для вогнутой функции f’’(x)≤0
Теорема 3. Если функция f(x) выпукла (вогнута) на отрезке [a,b], то на любом отрезке [x1,x2]⊂[a,b] график функции f(x) лежит не выше (не ниже) хорды, проходящей через точки графика с абсциссами x1 и x2.
Доказательство:
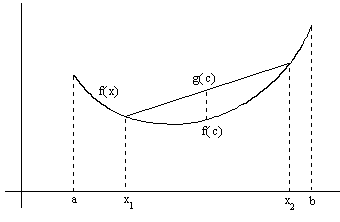
Рассмотрим выпуклую функцию. Уравнение хорды: проходящей через x1 и x2 имеет вид:
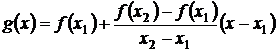 .
.
Рассмотрим точку c= αx1 + (1-α)x2, где aÎ[0,1]
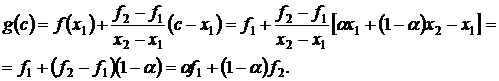
С другой стороны, по определению выпуклой функции имеем f(αx1 + (1-α)x2) ≤ αf1 + (1-α)f2; поэтому f(c) ≤ g(c) ч.т.д.
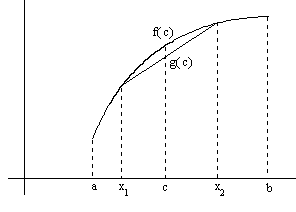
Для вогнутой функции доказательство аналогично.
Доказательство сходимости итерационного процесса рассмотрим для случая выпуклой (вогнутой) функции.
Теорема 4. Пусть задана непрерывная: дважды дифференцируемая функция f(x) на [a,b] и пусть f(a)f(b)<0, а f’(x) и f’’(x) сохраняют свои знаки на [a,b] (см. рис 1а,1б и рис 2а,2б). Тогда итерационный процесс метода хорд сходится к корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим для примера случай f(a)f’’(a)<0 (см рис 1а и 2а). Из формулы (9) следует, что xn > xn-1 так как (b-xn-1)>0, а fn-1/(fb-fn-1)<0. Это справедливо для любого n, то есть получаем возрастающую последовательность чисел
a≤x0<x1<x2<…<xn≤ b
Докажем теперь, что все приближения xn < ξ, где ξ - корень. Пусть xn-1 < ξ. Покажем, что xn тоже меньше ξ. Введем
xn=α·xn-1+(1-α)·b; ε=μ·αn-1+(1-μ)·b (3.11)
Имеем
y(xn)=α·fn-1+(1-α)·fb = f(ε) (3.12)
(то есть значение функции y(x) в точке xn на хорде [xn-1; b] совпадает с f(ξ)).
Так как f(ε)≤μ·fn-1+(1-μ)·fb, то из (3.12) следует
α·fn-1+(1-α)·fb≤μ·fn-1+(1-μ)·fb или α(fn-1-fb)≤μ(fn-1-fb) (3.13)
Для рис. 1а fn-1<fb, следовательно
α(fb-fn-1)≥μ(fb-fn-1) или α≥μ значит xn<ε, и т.д. (см. (3.11)).
Для рис 2а f(ε)≥μ·fn-1+(1-μ)·fb. Следовательно, из (3.12) получим
α·fn-1+(1-α)·fb≥μ·fn-1+(1-μ)·fb значит
α(fn-1-fb)≥μ(fn-1-fb) так как fn-1>fb → α>μ → xn≤ε и т.д.
Аналогичное доказательство для рис.1б и рис.2б. Таким образом, мы доказали, что последовательность чисел {xi} является сходящейся.
a≤x0<x1<x2<…<xn≤ξ≤ b (рис.1а,2а).
a≤ ξ<xn< … <x1<x0≤ x0≤ b (рис.1б,2б).
Это значит, что для любого ε можно указать такое n, что будет выполняться |xn - ξ |<ε. Теорема доказана.
Сходимость метода хорд линейная с коэффициентом 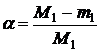 .
.
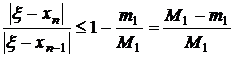 , (3.14)
, (3.14)
где m1=min|f’(x)|, M1=max|f’(x)|.
Это вытекает из следующих формул. Рассмотрим случай неподвижного конца b и f(b)>0.
Имеем из (3.9) 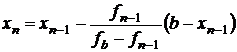 . Отсюда
. Отсюда
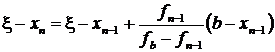 . Учитывая, что
. Учитывая, что 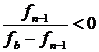 , мы можем записать
, мы можем записать 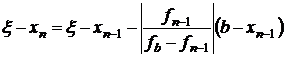 или
или
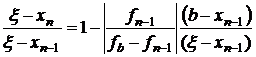 .
.
Заменяя в знаменателе правой части (ξ-xn-1) на (b-xn-1) и учитывая, что (ξ-xn-1)< (b-xn-1), получим 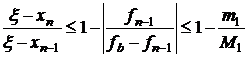 , что и требовалось доказать (см. неравенство (3.14)).
, что и требовалось доказать (см. неравенство (3.14)).
Доказательство сходимости для случая рис.3 (f’’(x) меняет знак; в общем случае как f’, так и f’’ могут менять знаки) более сложное и здесь не приводится.
Алгоритм метода хорд
Описание алгоритма метода хордШаг 1. Ввод a,b,ε.
Шаг 2. X:=a-f(a)×(b-a)/(f(b)-f(a)).
Шаг 3. Если dF2(b)×F(b)<0, то a:=x;
Если dF2(a)×F(a)<0, то b:=x;
Шаг 4. Пересчитать X по формуле шага 2.
Шаг 5. Выполнять шаг 3, пока abs(b-a)<=eps.
Шаг 4.Вывод результата – x.
Опишем назначение переменных и функций, используемых в процедуре
Hord
dF2 – значение второй производной в точке Х
F – значение функции в точке Х
Х0 – начальное значение Х
А – левая граница
В – правая граница
Е – точность вычислений
Fa – значение функции в точке А
Fb - значение функции в точке В
Представим в виде структурной схемы. Блок схема алгоритма метода хорд
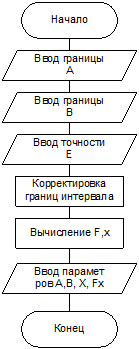
Для начала нам необходимо проверить границы интервала. Для этого разбиваем интервал на 10 частей и в цикле проверяем условие наличия корня:
Если условие выполняется, то корректируем границы
A:=A+i*(B-A)/10;
B:=A+(i+1)*(B-A)/10;
Однако, если корня нет – то выводим сообщение об ошибке.
Если кривая имеет на отрезке выпуклость (dF2(A)*F(A) > 0), то применяем следующий алгоритм. Пока разность значений корня будет больше заданной двигаемся влево применяя формулу
X := X0 - Fx*(X0 - A)/(Fx - Fa).
Если кривая имеет на отрезке вогнутость, то применяем следующий алгоритм. Пока разность значений корня будет больше заданной двигаемся вправо применяя формулу
X := X0 - Fx*(B - X0)/(Fb - Fx).
Реализация алгоритма метода хорд на Pascal
Procedure Hord(A,B:Real; E:Real; var X, Fx:Real;n:integer);
var
X0,Fa,Fb:real;
Begin
if dF2(A,n)*F(A,n) > 0 then
begin
X:=B;X0:=A;
Fa:=F(A,n);
while (Abs(X0-X)>E) do
begin
X0:=X;
Fx:=F(X0,n);
X:=X0-Fx*(X0-A)/(Fx-Fa);
end
end
else begin
X:=A;X0:=B;
Fb:=F(B,n);
while (Abs(X0-X)>E) do
begin
X0:=X;
Fx:=F(X0,n);
X:=X0-Fx*(B-X0)/(Fb-Fx);
end
end;
Fx:=F(X,n);
End;
Примеры решения
Пример 1. Найдем корни уравнения: ln(x)+(x+1)3 = 0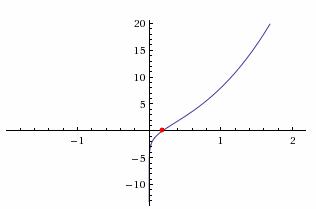
h0 = 0.1 + 0*(1-0.1)/10 = 0.1
h1 = 0.1 + (0+1)*(1-0.1)/10 = 0.19
Поскольку F(0.1)*F(0.19)<0, то корень лежит в пределах [0.1;0.19].
Вычисляем значения функций в точке a = 0.1.
f(0.1) = -0.972
f″(0.1) = -93.4
Поскольку f(a)·f″(a) > 0, то x0 = a = 0.1
Остальные расчеты сведем в таблицу.
| N | x | F(x) | h = F(x)*(x-a)/(f(x)-f(a)) |
| 1 | 0.19 | 0.02443 | 0.1878 |
| 2 | 0.1878 | 0.00338 | 0.1875 |
Пример 2. В задачах определить количество действительных корней уравнения f(x) = 0, отделить эти корни и, применяя метод хорд и касательных, найти их приближенные значения с точностью до 0.001.