Метод Ньютона
Метод Ньютона используется для нахождения корней функцииf(x) = 0. Если необходимо найти минимум функции f(x) → min методом Ньютона, то необходимо использовать данный калькулятор.
Назначение сервиса. Сервис предназначен для отыскания корней уравнений f(x) в онлайн режиме следующими методами:
- Метод хорд, Метод итераций, Комбинированный метод, Метод половинного деления (метод дихотомии)
- Метод золотого сечения, Модифицированный метод Ньютона, Метод секущих, Метод Ньютона (метод касательных)
Инструкция. Введите выражение F(x), нажмите Далее. Полученное решение сохраняется в файле Word. Также создается шаблон решения в Excel.
Правила ввода функции, заданной в явном виде
10•x•e2x= 10*x*exp(2*x)x•e-x+cos(3x)= x*exp(-x)+cos(3*x)x3-x2+3= x^3-x^2+3- Выражение
0.9*x=sin(x)+1необходимо преобразовать к виду: sin(x)+1-0.9*x. Аналогично,x^2-7=5-3xк виду x^2+3x-12.
см. также Решение нелинейных уравнений. Примеры решений.
Пусть дано уравнение f(x)=0, где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b. Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x). Число ξ называется корнем k-ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)= … =fk-1(ξ) = 0. Однократный корень называется простым.
Приближенное нахождение корней уравнения складывается из двух этапов:
- Отделение корней, то есть установление интервалов
[αi,βi], в которых содержится один корень уравнения.f(a)•f(b)<0, т.е. значения функции на его концах имеют противоположные знаки.f’(x)сохраняет постоянный знак, т.е. функция монотонна (эти два условия достаточны, но НЕ необходимы) для единственности корня на искомом отрезке).f”(x)сохраняет постоянный знак, т.е. функция выпукла вверх, либо – вниз.
- Уточнение приближенных корней, то есть доведение их до заданной точности.
Геометрическая интерпретация метода Ньютона (метод касательных)
Пусть корень ξ уравнения f(x)=0 отделен на отрезке [a,b]. Предположим мы нашли (n-1)-ое приближение корня xn-1. Тогда n-ое приближение xn мы можем получить следующим образом. Положимxn = xn-1 + hn-1 . (3.15)
Раскладывая в ряд f(x=ξ) в точке xn-1, получим
f(xn) = f(xn-1+hn-1) = f(xn-1) + f’(xn-1)hn-1=0
Отсюда следует
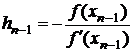 . (3.16)
. (3.16)
Подставим (3.16) в формулу (3.15), получим
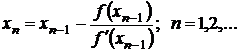 (3.17)
(3.17)
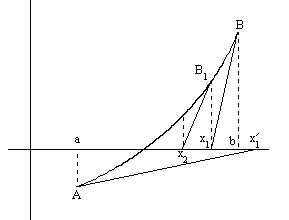
Рис.1. Геометрическая интерпретация метода Ньютона
Геометрически метод Ньютона эквивалентен замене дуги кривой y=f(x) касательной, проведенной в некоторой точке кривой (см. рис.1).
В точке B имеем f(x0)f’’(x0)>0. Здесь x0=b. Проведем касательную в точке B, получим на пересечении касательной осью OX точку x1. Далее проводим касательную в точке B1, получим точку x2 и т.д.
Если положить x0=a, то в точке x0 будем иметь f(x0)f’’(x0)<0. Тогда касательная в точке A пересекла бы ось OX в точке x’1, лежащей вне отрезка [a,b], то есть при таком выборе начальной точки, метод Ньютона оказывается расходящимся. Достаточные условия сходимости метода Ньютона определяются следующей теоремой.
Теорема 5. Если f(a)f(b)<0, причем f′(x) и f″(x) отличны от нуля и сохраняют определенные знаки при a≤x≤b, то исходя из начального приближения x0∈[a,b], удовлетворяющего неравенству
f(x0)f’’(x0)>0 (3.18)
можно вычислить методом Ньютона (3.17) единственный корень ξ уравнения f(x)=0 с любой степенью точности.
Доказательство: Пусть f(a)<0, f(b)>0, f′(x)>0, f″(x)>0, a≤x≤b. Согласно неравенству (3.18) в качестве точки x0 мы должны взять ту границу отрезка, для которой f(x0)>0, т.е. в данном случае т. b.
Итак, имеем x0>ξ. Докажем, что все приближения xn> ξ и следовательно все f(xn)>0. Пусть теперь xn-1> ξ. Положим ξ = xn-1 + (ξ-xn-1).
Применяя формулу Тейлора, получим
Так как f″(x)>0, то имеем
f(xn-1)+f′(xn-1)(ε-xn-1)<0 и, следовательно
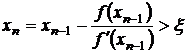 ч.т.д. (3.19)
ч.т.д. (3.19)
Из (3.19) учитывая знаки f(xn-1) и f′(xn-1) имеем xn<xn-1, то есть получаем ограниченную монотонную убывающую последовательность x0>x1> ... >xn>xn+1>ε. Следовательно, существует
Переходя к пределу в формуле (3.17) получим
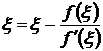 , то есть f(ξ)=0, и следовательно, ξ- корень ,ч.т.д.
, то есть f(ξ)=0, и следовательно, ξ- корень ,ч.т.д.
Оценим скорость сходимости метода Ньютона. Из (3.17) следует
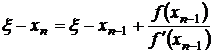 . (3.20)
. (3.20)
Представим f(ξ) в виде
Подставим (3.21) в (3.20), получим
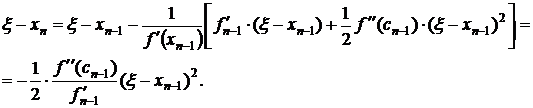
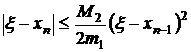 . (3.22)
. (3.22)
Здесь
Таким образом, скорость сходимости метода Ньютона квадратичная.
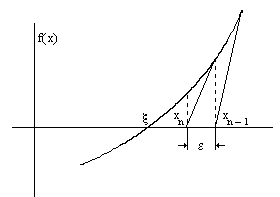
Рис.2
Критерий завершения итерационного процесса имеет вид
Замечание. В общем случае совпадение с точностью до ε двух последовательных приближений xn-1 и xn не гарантирует, что с той же точностью совпадет xn и ξ (см. рис. 2). Поэтому целесообразно проверять кроме разности |xn – xn-1|<ε также значение функции f(xn): |f(xn)|< ε1.
Пример. f(x) = x4-3x3+75x-10000=0.
Найти отрицательный корень с пятью верными знаками.
Решение: Полагая x=0, -10, -100, получим f(0)=-104, f(-10) = -150, f(-100) ≈ 108. Таким образом -100<ξ<-10. Сузим интервал, так как f(-11)=3433, то -11< ξ <-10.
В интервале [-11, -10] f(x)<0, f’’(x)>0. Так как f(-11)f’’(-11)>0, то x0=-11.
Последовательные приближения даны в таблице.
| n | xn | f(xn) | f’(xn) | hn=- f(xn)/ f’(xn) |
| 0 | -11 | 3453 | -5183 | 0.7 |
| 1 | -10.3 | 134.3 | -4234 | 0.03 |
| 2 | -10.27 | 37.8 | -4196 | 0.009 |
| 3 | -10.261 | 0.2 | ||
| 4 | -10.260 | <0 |
Метод золотого сечения
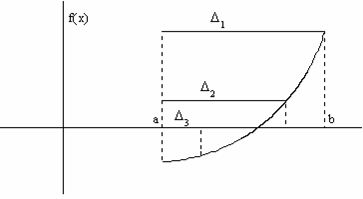
Точки деления интервала выбираются таким образом, чтобы отношение длин подынтервалов удовлетворяло соотношению (см. рис.)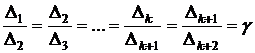 . (3.32)
. (3.32)Так как Δk = Δk+1 + Δk+2, то имеем
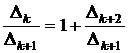 . (3.33)
. (3.33)
С учетом (3.32) из (3.33) получим уравнение
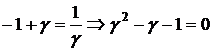 ,
,корнем которого является золотое сечение.
Скорость сходимости МЗС имеет порядок с коэффициентом 1/γ = γ -1 = 0.618.