Комбинированный метод
Назначение сервиса. С помощью этого сервиса в онлайн режиме выполняется поиск корней функции комбинированным методом. Решение оформляется в формате MS Word.Правила ввода функции
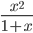≡ x^2/(1+x)
cos2(2x+π) ≡ (cos(2*x+pi))^2
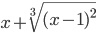≡ x+(x-1)^(2/3)
Алгоритм комбинированного метода
Пусть f(a)f(b)<0, а f’(x) и f″(x) сохраняют знаки на [a,b]. Объединяя метод хорд и метод Ньютона, можно ускорить сходимость итерационного процесса поиска корня. В результате мы получаем комбинированный метод, на каждом шаге которого находим значение обоих границ интервалов, внутри которых содержится корень. Также как и в методе хорд, рассмотрим следующие ситуации1. Если f″(b0)f(b0)>0 (то есть bn - неподвижен, рис.4) то
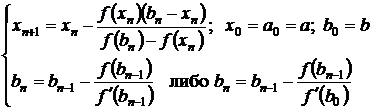(3.30)f″(x)>0, f″(b)·f(b)>0,
f″(x)<0, f″(b)·f(b)>0,
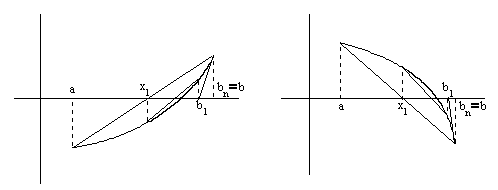
2) Если f″(a0)f(a0)>0 (an - неподвижен, см.рис.5), то
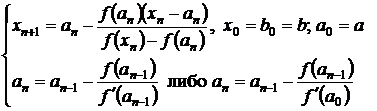(3.31)Здесь f(an)f(xn)<0.
f″(x)<0, f″(a)f(a)>0 f″(x)>0, f″(a)f(a)>0
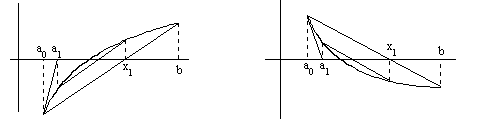
Рис.5а Рис.5б
