Метод Фибоначчи
Для получения решения в онлайн режиме необходимо заполнить исходные данные.Правила ввода функции
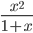 ≡ x^2/(1+x)
≡ x^2/(1+x)
cos2(2x+π) ≡ (cos(2*x+pi))^2
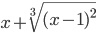 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)
Метод дихотомии не эффективен в том смысле, что для конечного фиксированного числа n вычислений значений функции, он не приводит к наименьшему возможному интервалу. Эффективным методом в этом смысле является метод Фибоначчи.
Важнейшая особенность этого метода состоит в том, что он позволяет для заранее заданного числа вычислений функции построить оптимальную процедуру поиска минимума унимодальной функции.
Предположим, что заданный начальный интервал неопределенности [a1,b1], [ai,bi] является интервалом неопределенности, полученным на i - той итерации. Рассмотрим две точки λi и μi из интервала [ai,bi], заданные с помощью соотношений
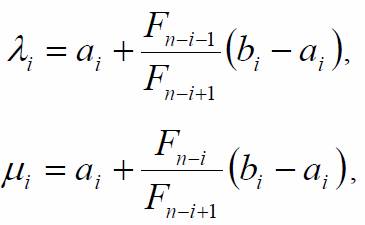
где n - заданное число вычислений функции; Fk - последовательность чисел Фибоначчи, заданная с помощью рекуррентной формулы
Fk+1 = Fk + Fk-1 , k = 1,2, …, где F0= F1 = 1
Новый интервал неопределенности (ai+1,bi+1) равен (λi,bi), если f(λi) > f(μi), и равен (ai , μi), если f(λi) < f(μi). Тогда в первом случае, новый интервал неопределенности имеет длину
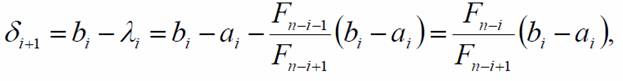
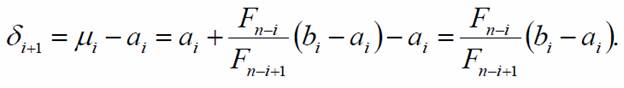
Если ε есть точность вычисления значения функции, n – максимально возможное число вычислений функции, то конечный интервал неопределенности будет равен
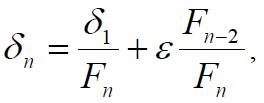
т.е. сократится в Fn раз.
Пример. Минимизировать функцию f(x) на отрезке [0;8]. Известно, что можно выполнить n=6 вычислений функции.
Найдем минимум функции:
4.2•x2+23/x = 0
Используем для этого Метод Фибоначчи.
Важнейшая особенность этого метода состоит в том, что он позволяет для заранее заданного числа вычислений функции построить оптимальную процедуру поиска минимума унимодальной функции.
Предположим, что заданный начальный интервал неопределенности [a1,b1], [ai,bi] является интервалом неопределенности, полученным на i-той итерации. Рассмотрим две точки λi и μi из интервала [ai,bi], заданные с помощью соотношений:
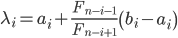
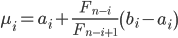
где n - заданное число вычислений функции; Fk - последовательность чисел Фибоначчи, заданная с помощью рекуррентной формулы:
Fk+1 = Fk + Fk-1, k = 1,2, … , где F0 = F1 = 1
Новый интервал неопределенности (ai+1,bi+1) равен (λi,bi), если f(λi) > f(μi), и равен (ai, μi), если f(λi) < f(μi). Тогда в первом случае, новый интервал неопределенности имеет длину: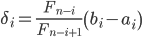
Отсюда следует, что в любом случае на i-той итерации интервал неопределенности сжимается в Fn-i/Fn-i+1 раз. На (i+1)-ой итерации либо λi+1 = μi, либо μi+1 = λi. Поэтому на каждом шаге вычисляется только одно новое значение функции. На (n-1)-ой итерации λn-1 = μn-1,и значение функции не вычисляется.
Если ε есть точность вычисления значения функции, n – максимально возможное число вычислений функции, то конечный интервал неопределенности будет равен: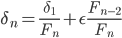
Решение.
Последовательность чисел Фибоначчи имеет вид: 1,1,2,3,5,8,13,21
Итерация 1.
Вычислим точки
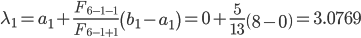
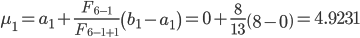
Так как f(λ1) < f(μ1), то сокращаем интервал неопределенности и принимаем на второй итерации:
a2 = a1 = 0; b2 = μ1 = 4.9231
Итерация 2.
Вычислим точки
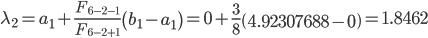
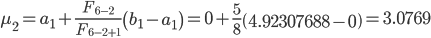
Так как f(λ2) < f(μ2), то сокращаем интервал неопределенности и принимаем на второй итерации:
a3 = a2 = 0; b3 = μ2 = 3.0769
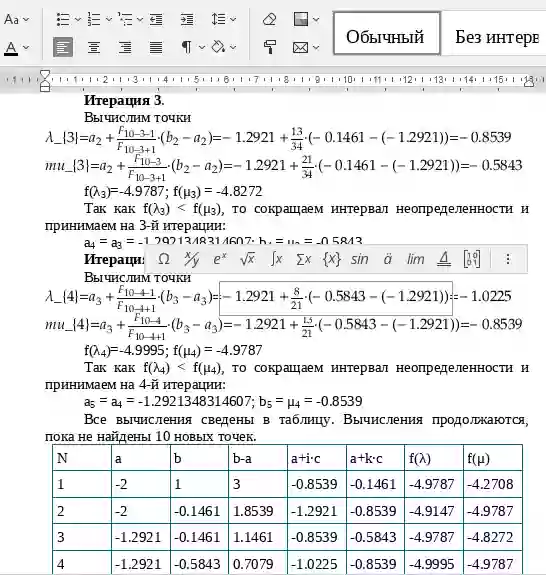
Итерация 3.
Вычислим точки
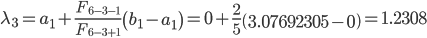
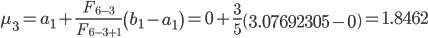
Так как f(λ3) < f(μ3), то сокращаем интервал неопределенности и принимаем на второй итерации:
a4 = a3 = 0; b4 = μ3 = 1.8462
Итерация 4.
Вычислим точки
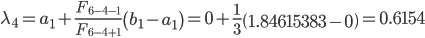
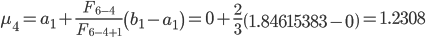
f(λ4) = 38.9655; f(μ4) = 25.0496
Так как f(λ4) > f(μ4), то сокращаем интервал неопределенности и принимаем на второй итерации:
a5 = λ4 = 0.6153846; b5 = b;4 = 1.8462
Все вычисления сведены в таблицу. Вычисления продолжаются, пока не найдены 6 новых точек.
| N | a | b | b-a | a+i*c | a+k*c | f(l) | f(m) |
| 1 | 0 | 8 | 8 | 3.0769 | 4.9231 | 47.2383 | 106.466 |
| 2 | 0 | 4.9231 | 4.9231 | 1.8462 | 3.0769 | 26.7731 | 47.2383 |
| 3 | 0 | 3.0769 | 3.0769 | 1.2308 | 1.8462 | 25.0496 | 26.7731 |
| 4 | 0 | 1.8462 | 1.8462 | 0.6154 | 1.2308 | 38.9655 | 25.0496 |
| 5 | 0.6154 | 1.8462 | 1.2308 | 1.2308 | 1.2308 | 25.0496 | 25.0496 |
| 6 | 0.6154 | 1.8462 | 1.2308 | 0.6154 | 1.8462 | 38.9655 | 26.7731 |
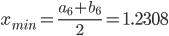
f(xmin) = 25.0496
Ответ: x = 1.2308; F(x) = 25.0496