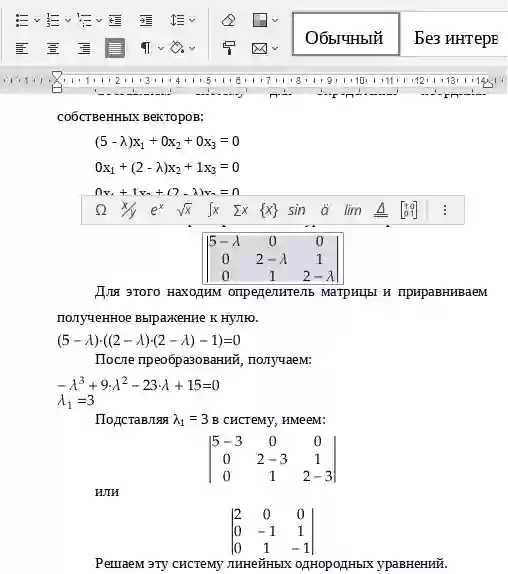
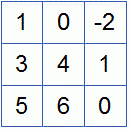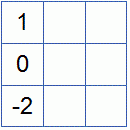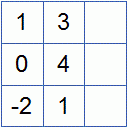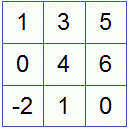
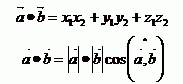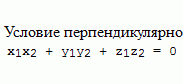Собственные числа матрицы линейного оператора
Собственный вектор оператора A - ненулевой вектор X, переводящий X в коллинеарный ему вектор, то есть AX = λX. где λ - собственное значение или собственное число оператора A.Назначение сервиса. Калькулятор предназначен для нахождения в онлайн режиме собственных чисел и собственных векторов матрицы. (см. пример решения)
Инструкция. Выберите размерность матрицы. Полученное решение сохраняется в файле Word.
Составляем систему для определения координат собственных векторов:
(17 - λ)x1 + 6x2 = 0
6x1 + (8 - λ)x2 = 0
Составляем характеристическое уравнение и решаем его:
λ2 -25 λ + 100 = 0
D = (-25)2 - 4 • 1 • 100 = 225
-3x1 + 6y1 = 0
6x1-12y1 = 0
или
-3x1 + 6y1 = 0
Собственный вектор, отвечающий числу λ1 = 20 при x1 = 2: x1 = (2,1)
В качестве единичного собственного вектора принимаем вектор:
где
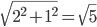- длина вектора x1.
Координаты второго собственного вектора, соответствующего второму собственному числу λ2 = 5, находим из системы:
12x1 + 6y1 = 0
6x1 + 3y1 = 0
или
12x1 + 6y1 = 0
Значения собственных чисел и векторов используются при решении систем дифференциальных уравнений.
