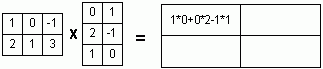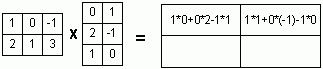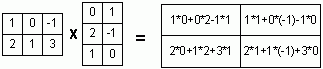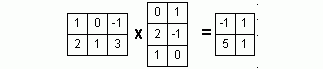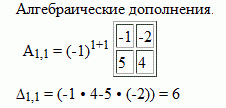Собственные числа матрицы. Примеры решений

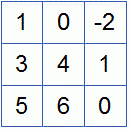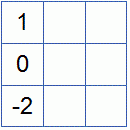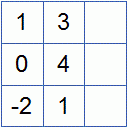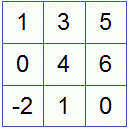
Пример 1. Найти собственные числа и собственные векторы матрицы

Решение находим с помощью калькулятора. Составим характеристическое уравнение:

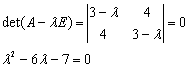
Отсюда собственные числа данной матрицы: λ₁=-1, λ₂=7
Найдем собственные векторы, соответствующие этим собственным значениям
Подставим собственное число λ₁=-1 в систему однородных уравнений (A-λE)X=0 и найдем ее нетривиальное решение.

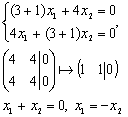
Ранг матрицы r=1, ФСР содержит (n-r)=1 решение. Пусть x₂=1, тогда x₁=-1. Получаем собственный вектор

Рассмотрим собственное значение λ₂=7

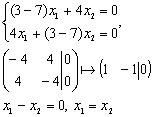
Положим x₂=1, тогда x₁=1. Получаем собственный вектор

Пример 2. Найти собственные числа и собственные векторы матрицы

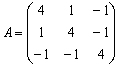
Решение. Составим характеристическое уравнение:

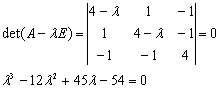
Собственные числа данной матрицы: λ_1,2=3, λ₃=6
Найдем собственные векторы, соответствующие λ=3.


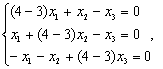
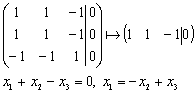
Ранг матрицы r=1, ФСР содержит (n-r)=3-1=2 решения. Зададим два набора значений свободных переменных и составим два собственных вектора

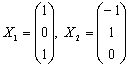
Найдем собственные векторы, соответствующие λ=6.


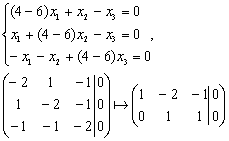
Ранг матрицы r=2, ФСР содержит (n-r)=3-1=1 решение. Зададим значение свободной переменной и составим собственный вектор

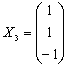
Перейти к онлайн решению своей задачи