Вычисление определителя матрицы методом декомпозиции
Назначение сервиса. Сервис предназначен для LU-разложения матрицы, которое можно использовать для вычисления определителя. Все вычисления проходят в онлайн режиме.A=B×C
|
|
|
|
Алгоритм декомпозиции основан на идее представления исходной матрицы в виде произведения двух треугольных матриц. Пусть задана квадратная матрица:
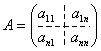
Представим A в виде:
где
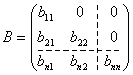
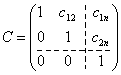 .
.
Тогда
 .
.

Данный алгоритм представляют собой алгоритм разложения квадратной матрицы на две треугольные матрицы. см. также вычисление определителя методом Гаусса.
Пример №1. Для матрицы:
| A = |
|
Решение. Покажем пример вычислений нескольких значений матриц B и C.
Вычисляем значение элемента b11 = 5
c11 = 5/5 = 1
c12 = 4/5 = 0.8
c13 = 3/5 = 0.6
Вычисляем значение элемента b21 = 21
Вычисляем значение элемента b22 = -2 - (21 • 0.8) = -18.8
c22 = -18.8/-18.8 = 1
c23 = -6.6/-18.8 = 0.3511
Вычисляем значение элемента b31 = 5
Вычисляем значение элемента b32 = 4 - (5 • 0.8) = 0
Вычисляем значение элемента b33 = 0 - (5 • 0.6 + 0 • 0.3511) = -3
c33 = -3/-3 = 1
| B = |
|
| C = |
|
detA = 5 • (-18.8) • (-3) = 282
Ответ: определитель равен 282.
Пример №2. Покажем пример вычислений нескольких значений матриц B и C.
Вычисляем значение элемента b11=-1
c11=-1/(-1)=1
c12=4/(-1)=-4
c13=3/(-1)=-3
Вычисляем значение элемента b21=2
Вычисляем значение элемента b22=0 - (2 • -4)=8
c22=8/8=1
c23=15/8=1.88
Вычисляем значение элемента b31=4
Вычисляем значение элемента b32=5 - (4 • -4)=21
Вычисляем значение элемента b33=-3 - (4 • -3 + 21 • 1.88)=-30.38
c33=-30.38/(-30.38)=1
| B= |
|
| C= |
|
detA=(-1) • 8 • (-30.38) = 243
Ответ: 243