Решение СЛАУ методом Зейделя
Назначение сервиса. Сервис предназначен для решения СЛАУ в онлайн режиме методом Зейделя. Дополнительно генерируется шаблон решения в Excel. Метод Зейделя представляет собой модификацию метода простой итераций.Инструкция. Выберите количество переменных, нажмите Далее.
Метод Зейделя представляет собой модификацию метода простой итераций.
Пусть дана приведённая система:
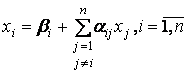
и известно начальное приближение (x01, x02,...,x0n)=x0. Основная идея заключается в том,
что при вычислении (k+1) - го приближения неизвестной xi учитываются уже вычисленные ранее (k+1) - приближение неизвестных x1, x2, .., xi-1.
Итерационная схема имеет вид:

Положим α = B + C, где
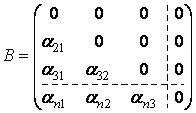 ;
;  .
.
Тогда процесс Зейделя в матричном виде можно записать как:
xk+1 = B xk +1 + C xk + β
Процесс Зейделя для нормальной системы
Рассмотрим один из способов преобразования системы:позволяющий всегда получать сходящийся процесс Зейделя. Помножим (1) слева на AT
где C = ATA; d = ATb.
Систему (2) принято называть нормальной. (Такая система получается при использовании МНК)
Нормальная система обладает рядом замечательных свойств:
- матрица С – симметрическая;
- все элементы главной диагонали cij > 0;
- матрица С - положительно определена.
Достаточные условия сходимости итерационной последовательности
Достаточные условия сходимости итерационной последовательности приближенных решений системы и оценка погрешности проводятся по тем же формулам, что и в методе простой итерации.Пример №1. Рассмотрим вычисление двух приближений по методу Зейделя для примера, решенного выше для метода простой итерации и оценим погрешность.
Вычисления будем проводить по формулам:
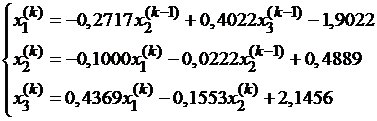
x(1)=(-1,9022;0,6791;1,2091), x(2)=(-1,6004;0,6291;1,3498).
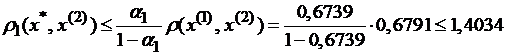
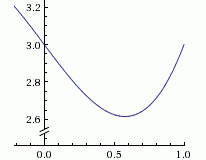
Пример №2. Система двух Линейных Алгебраических Уравнения (СЛАУ) с двумя неизвестными задана своей расширенной матрицей. Решите СЛАУ методом Зейделя с точностью до 0.001. Поменяйте порядок уравнений в СЛАУ и решите полученную таким образом СЛАУ тем же методом Зейделя. Постройте графики уравнений СЛАУ в обоих СЛАУ в обоих случаях и покажите на них первые три-четыре итерации.
| -4 | 4 | -3 |
| 4 | 7 | -4 |
Пример №3. Методом Зейделя решить с точностью 0,001 систему линейных уравнений, приведя ее к виду, удобному для итерации.
3.6x1 + 1.8x2 - 4.7x3 = 3.8
2.7x1 - 3.6x2 + 1.9x3 = 0.4
1.5x1 + 4.5x2 + 3.3x3 = -1.6
Решение. Умножаем матрицы ATA.
| ATA= |
|
Умножаем матрицы ATb.
| ATb= |
|
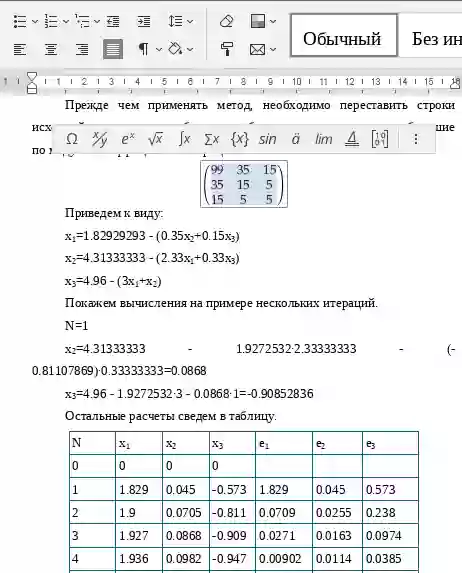
Приведем к виду:
x1=0.55+0.16x2-0.3x3
x2=-0.0494+0.0963x1-0.0123x3
x3=-0.61-0.19x1-0.0123x2
Покажем вычисления на примере нескольких итераций.
N=1
x1=0.55 - 0 • 0.16 - 0 • (-0.3)=0.55
x2=-0.0494 - 0.55 • 0.0963 - 0 • (-0.0123)=-0.1
x3=-0.61 - 0.55 • (-0.19) - (-0.1) • (-0.0123)=-0.51
N=2
x1=0.55 - (-0.1) • 0.16 - (-0.51) • (-0.3)=0.41
x2=-0.0494 - 0.41 • 0.0963 - (-0.51) • (-0.0123)=-0.0952
x3=-0.61 - 0.41 • (-0.19) - (-0.0952) • (-0.0123)=-0.54
N=3
x1=0.55 - (-0.0952) • 0.16 - (-0.54) • (-0.3)=0.4
x2=-0.0494 - 0.4 • 0.0963 - (-0.54) • (-0.0123)=-0.0946
x3=-0.61 - 0.4 • (-0.19) - (-0.0946) • (-0.0123)=-0.54
Остальные расчеты сведем в таблицу.
| N | x1 | x2 | x3 | e1 | e2 | e3 |
| 0 | 0 | 0 | 0 | |||
| 1 | 0.55 | -0.1 | -0.51 | 0.55 | 0.1 | 0.51 |
| 2 | 0.41 | -0.0952 | -0.54 | -0.14 | -0.0071 | 0.0259 |
| 3 | 0.4 | -0.0946 | -0.54 | -0.00899 | -0.000546 | 0.00167 |
| 4 | 0.4 | -0.0946 | -0.54 | -0.000594 | -3.7E-5 | 0.000111 |
Пример №4. Выполнить три итерации по методу Зейделя для системы уравнений Ax=b (не переставляя строк). В качестве начального приближения взять нулевой вектор. Изобразить графически поведение итерационного процесса. Сопоставить его сходимость с выполнением достаточных условий сходимости метода.