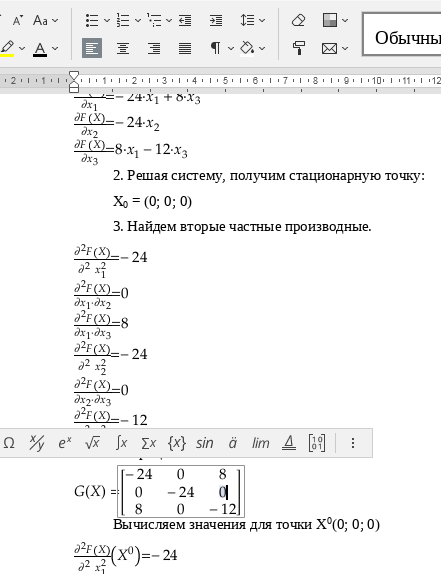
Матрица Гессе
Назначение сервиса. Онлайн-калькулятор используется для нахождения матрицы Гессе и определения вида функции (выпуклая или вогнутая). Решение оформляется в формате Word. Для функции одной переменной f(x) определяются интервалы выпуклости и вогнутости.- Все переменные выражаются через x1,x2,x3
- Все математические операции выражаются через общепринятые символы +, -, *, /, ^
- Корень квадратный √¯ ≡ sqrt, степень корня ≡ x^(2/3), (x-1)^(1/3)
число π ≡ pi, число e ≡ exp(1), ∞ ≡ infinity
ex = exp(x), log5(x) ≡ log(x,5)
Тригонометрические функции: cos(x), sin(x), tg(x), ctg(x), arccos(x), arcsin(x), arctg(x), arcctg(x)
Дважды непрерывно дифференцируемая функция f(x) является выпуклой (вогнутой) тогда и только тогда, когда матрица Гессе функции f(x) по x положительно (отрицательно) полуопределена для всех x (см. точки локальных экстремумов функции многих переменных).
Критические точки функции:
- если гессиан положительно определён, то x0 — точка локального минимума функции f(x),
- если гессиан отрицательно определён, то x0 — точка локального максимума функции f(x),
- если гессиан не является знакоопределённым (принимает как положительные, так и отрицательные значения) и невырожден (det G(f) ≠ 0), то x0 — седловая точка функции f(x).
Критерии определенности матрицы (теорема Сильвестра)
Положительная определенность:- все диагональные элементы матрицы должны быть положительны;
- все ведущие главные определители должны быть положительны.
Положительная полуопределенность:
- все диагональные элементы неотрицательны;
- все главные определители неотрицательны.
Квадратная симметрическая матрица порядка n, элементами которой являются частные производные целевой функции второго порядка, называется матрицей Гессе и обозначается:
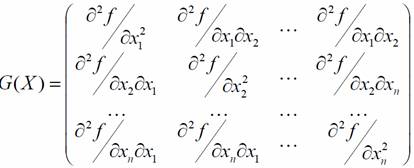
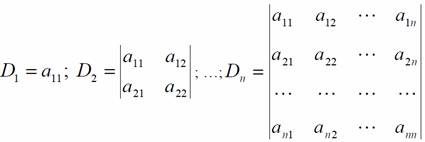
Отрицательная определенность.
Для того чтобы симметрическая матрица была отрицательно определена, необходимо и достаточно, чтобы имели место неравенства:
(-1)k Dk> 0, k =1,.., n.
Другими словами, для того, чтобы квадратичная форма была отрицательно определённой, необходимо и достаточно, чтобы знаки угловых миноров матрицы квадратичной формы чередовались, начиная со знака минус. Например, для двух переменных, D1 < 0, D2 > 0.
Если гессиан полуопределен, то это может быть и точка перегиба. Нужны дополнительные исследования, которые могут быть проведены по одному из следующих вариантов:
- Понижение порядка. Делается замена переменных. Например, для функции двух переменных это
y=x, в итоге получаем функцию одного переменного x. Далее исследуется поведение функции на прямых y=x и y=-x. Если в первом случае функция в исследуемой точке будет иметь минимум, а в другом случае максимум (или наоборот), то исследуемая точка представляет собой седловую точку. - Нахождение собственных значений гессиана. Если все значения положительные, функция в исследуемой точке имеет минимум, если все отрицательные – имеется максимум.
- Исследование функции f(x) в окрестности точки ε. Переменные x заменяются на x0+ε. Далее необходимо доказать, что функция f(x0+ε) от одной переменной ε, либо больше нуля (тогда x0 точка минимума), либо меньше нуля (тогда x0 точка максимума).
Примечание. Чтобы найти обратный гессиан достаточно найти обратную матрицу.
Пример №1. Какие из следующих функций являются выпуклыми или вогнутыми: f(x) = 8x12+4x1x2+5x22.
Решение. 1. Найдем частные производные.
2. Решим систему уравнений.
-4x1+4x2+2 = 0
4x1-6x2+6 = 0
Получим:
а) Из первого уравнения выражаем x1 и подставляем во второе уравнение:
x2 = x2+1/2
-2x2+8 = 0
Откуда x2 = 4
Данные значения x2 подставляем в выражение для x1. Получаем: x1 = 9/2
Количество критических точек равно 1.
M1(9/2;4)
3. Найдем частные производные второго порядка.
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(9/2;4)
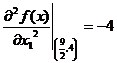
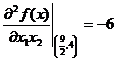
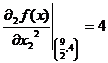
Строим матрицу Гессе:
D1 = a11 < 0, D2 = 8 > 0
Поскольку диагональные миноры имеют различные знаки, то о выпуклости или вогнутости функции ничего сказать нельзя.
Пример №2. Выяснить, является ли функция f(x) = 2x12 + x22 + sin(x1 + x2) выпуклой в пространстве R2.
Решение. Дважды дифференцируемая функция является выпуклой в пространстве R2, если главные угловые миноры матрицы Гессе неотрицательны. Запишем матрицу Гессе – матрицу вторых производных:
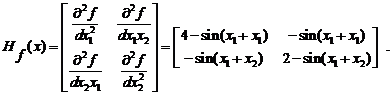
Пример №3. Является ли функция f(x) = x1+2*x1*x2+4*x2 выпуклой, вогнутой?
Решение. 1. Найдем частные производные.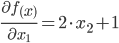 
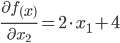
2. Решим систему уравнений.
2•x2+1 = 0
2•x1+4 = 0
Получим:
Количество критических точек равно 2.
M1(0;-1/2), M2(-2;0)
3. Найдем частные производные второго порядка.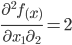
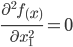
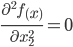
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(0;-1/2)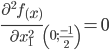
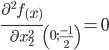
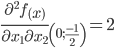
Строим матрицу Гессе:
|
D1 = a11 = 0, то вопрос о вогнутости или выпуклости функции остается открытым.
Вычисляем значения для точки M2(-2;0)
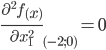
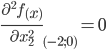
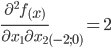
Строим матрицу Гессе:
|
D1 = a11 = 0, то вопрос о вогнутости или выпуклости функции остается открытым.
Пример №4. Выяснить, является ли функция 
выпуклой в пространстве R2.
Решение. Запишем матрицу Гессе – матрицу вторых производных:
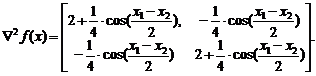
Угловые миноры равны:
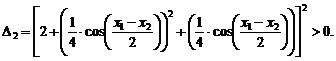
Таким образом, D1> 0, D2 > 0 при всех значениях x∈R2, т.е. функция f(x) выпукла.