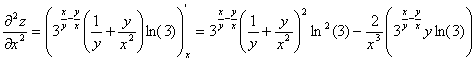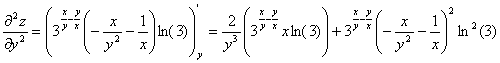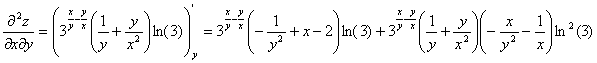Частные производные

Частной производной по x функции z = f(x,y) в точке A(x₀,y₀) называется предел отношения частного приращения по x функции в точке A к приращению ∆x при стремлении ∆x к нулю.
Частные производные функции z(x,y) находятся по следующим формулам: $Частные производные$
Вторые частные производные функции z(x,y) находятся по формулам:
$Вторые частные производные$
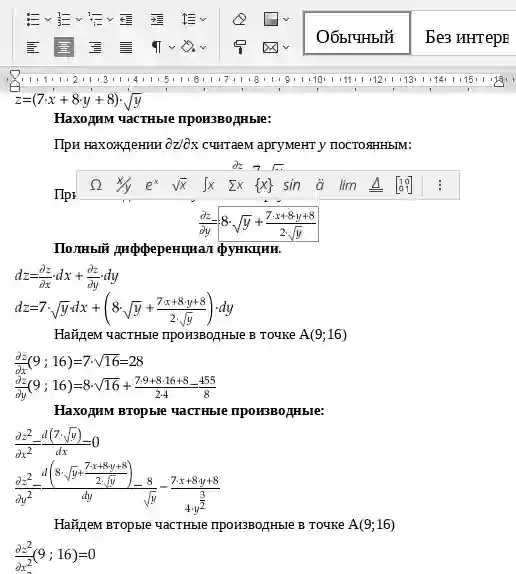
Смешанные частные производные функции z(x,y) находятся по формулам: $Смешанные частные производные$

Назначение сервиса. Сервис используется для нахождения частных производных функции (см. пример).

Правила ввода функции, заданной в явном виде

Вводить можно как с левой частью, так и без нее. Например, f(x;y)=x^2/(x+y) или x^2/(x+y).
Если дифференцирование происходит по переменным, отличных от x и y, левая часть обязательна. Например, f(p;r)=(cos(2*p+r))^2.

Правила ввода функции, заданной в неявном виде

Вводить можно как с левой частью, так и без нее. Например, f(x;y;z)=z+(x-y)^(2/3) или z+(x-y)^(2/3).
Если дифференцирование происходит по переменным, отличных от x, y и z, левая часть обязательна. Например, f(p;r;q)=q*(cos(2*p+r))^2.

Скачать пример оформления

Вместе с этим калькулятором также используют следующие:

Точки разрыва функции Производная функции Найти градиент функции gradu(M0) и du/dl(M0) Экстремум функции двух переменных Вычисление интегралов

Частные производные используются, например, при нахождении полного дифференциала и экстремумов функции.

Частные производные функции нескольких переменных

Ели одному из аргументов функции z = f(x,y) придать приращение, а другой аргумент не изменять, то функция получит частное приращение по одному из аргументов: Δ_xz=f(x+Δ_x,y)-f(x,y) – это частное приращение функции z по аргументу x; Δ_yz=f(x,y+Δ_y)-f(x,y) – это частное приращение функции z по аргументу у.
Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:

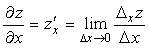– это частная производная функции z по аргументу x;

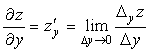– это частная производная функции z по аргументу у.
Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.

Пример 1. z=2x⁵+3x²y+y²–4x+5y-1

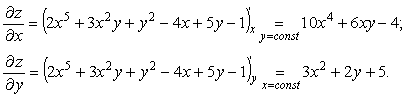
Пример 2. Найти частные производные функции z = f(x;y) в точке A(x₀;y₀).

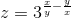
Находим частные производные:

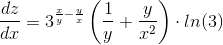
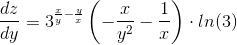
Найдем частные производные в точке А(1;1)

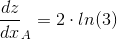
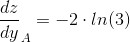
Находим вторые частные производные: