Примеры нахождения частных производных
Задача 2. Найти частные производные
, 
и 
, если переменные x, y, и z связаны равенством 4x2 y ez – cos(x3 – z) + 2y2 + 3x = 0.
Решение находим с помощью калькулятора.
Для F(x, y, z) = 4x2 y ez – cos(x3 – z) + 2y2 + 3x получаем:
F’x= (4x2 yez – cos(x3 – z) + 2y2 + 3x)’x = [считаем y и z постоянными] =
= 8x y ez + sin( x3 – z)3x2 + 3 = 8x y ez + 3x2 sin( x3 – z) + 3;
F’y= (4x2 y ez – cos(x3 – z) + 2y2 + 3x)’y = [считаем x и z постоянными] =
= 4x2 ez + 4y;
F’z = (4x2 y ez – cos(x3 – z) + 2y2 + 3x)’z = [считаем x и y постоянными] =
= 4x2 y ez – sin (x3 – z).
По формулам находим частные производные:
; 
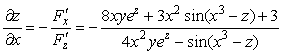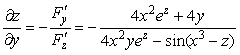
и по формуле (3) получаем:
.
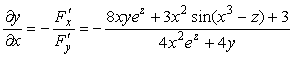Ответы:
; 
.
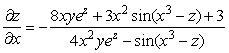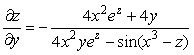
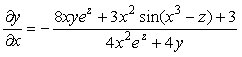Задание. Найти частные производные функции z в точке A(-1;0).
z = ln(x2+y2)+y/x
Решение.
Находим частные производные:
Задание №2. Найти частные производные 1-го и 2-го порядка.
z = x3 + 3x2y – sin(xy)
Скачать решение
Задача 1. Дана функция z = f(x,y). Требуется:
1) найти частные производные dz/dx и dz/dy;
2) найти полный дифференциал dz;
3) показать, что для данной функции справедливо равенство: d2z/dxdy = d2z/dydx.
Пример 1. Показать, что функция 
удовлетворяет уравнению 
.
Решение.
Найдем частные производные 
и 
.
,
.
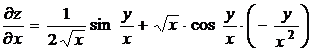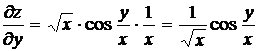Подставим их в уравнение
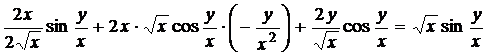
Получим тождество. Следовательно, функция z удовлетворяет данному уравнению.
Пример 2. Дана функция 
и две точки A(4;2 )и B(4.03;1.96). Требуется: 1) вычислить значение функции в точке В;
2) вычислить приближенное значение функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом;
3) оценить в процентах относительную погрешность, возникшую при замене приращения функции ее дифференциалом.
Решение.
Итак, z0=5, z≈z0+df(A);
.
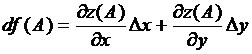Найдем
. 
, 
;
, 
;
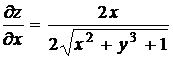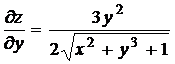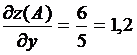f(4.03;1.96)=≈5+0.8·0.03+1.2·(-0.04)=5.072.
;
.
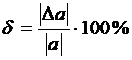