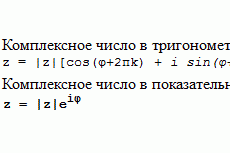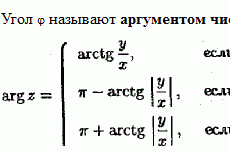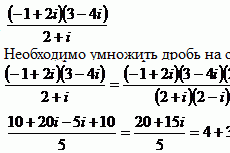Функция Лагранжа для задачи линейного программирования. Понятие седловой точки функции Лагранжа
Возьмем пару двойственных задач ЛП.| Прямая задача
| Двойственная задача
| ||
| Запишем в другом виде | |||
где yi– двойственная оценка для прямой задачи; xj– двойственная оценка для двойственной задачи.
Распространим функцию Лагранжа на задачи, в которых ограничения не обязательно имеют форму равенств. Запишем функции Лагранжа для прямой и двойственной задач:
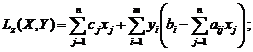 (1)
(1)
Из (1) – (2) следует, что для прямой ЗЛП двойственные оценки yi служат множителями Лагранжа, для двойственной ЗЛП множителями Лагранжа являются переменные xj Сложив почленно (1) и (2), получим LZ(X,Y) = -Lf(Y,X).
Определение. Функция L(X,Y) имеет в точке (X0, Y0) седловую точку, если
L(X, Y0) ≤ L(X0, Y0)≤ L(X0, Y) (3)
для всех X из ε>0 - окрестности X0 и всех Y из ε>0 –окрестности Y0. Если неравенства (3) выполняются для всех X и Y из области определения функции L(X,Y) то она имеет глобальную седловую точку (X0,Y0). Оптимальные решения пары двойственных задач ЛП образуют седловую точку функции Лагранжа (1). Геометрическая интерпретация седловой точки функции Лагранжа показана на рисунок.
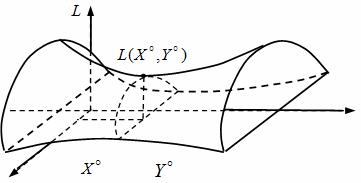
Рисунок - Геометрическая интерпретация седловой точки
Где находятся точки X0 и Y0?
Существует следующая теорема.
Теорема. Чтобы план X* был оптимальным решением прямой задачи ЛП, необходимо и достаточно, чтобы существовал такой вектор Y0 ≥ 0 когда точка (X0,Y0) была бы седловой точкой функции Лагранжа Lz(X,Y), т.е. для всех X ≥ 0 и Y ≥ 0:
LZ(X,Y0) ≤ L(X0,Y0)≤ L(X0,Y0)
![]()
![]()
![]()
т.е. задача определения оптимальных решений пары двойственных задач свелась к нахождению максимина или минимакса функции Лагранжа.