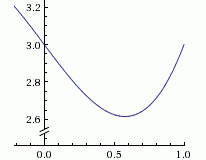
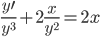Особенности задач нелинейного программирования

Нелинейное программирование занимается оптимизацией моделей задач, в которых либо ограничения q_i(x) либо целевая функция Z(X) либо то и другое нелинейны.
Найти max(min)=Z=z(X)
в области

где R – отношение порядка (=, ≥, ≤), Ω– область допустимых решений; b_i– константа, i=1,m;
X=(x₁,…,x_n)={x_j}, j=1..n – план или вектор управления.
Для выяснения трудностей решения задач данного класса, порождаемых нелинейностью, сопоставим задачи линейного и нелинейного программирования. Можно указать три характерные особенности для каждого класса.

Задачи линейного программирования	Задачи нелинейного программирования
1. Область Ω допустимых планов – *выпуклое множество* с конечным числом угловых (крайних) точек.	1. Множество Ω допустимых планов может быть *невыпуклым, несвязным*, иметь бесконечное число крайних точек.
2. Экстремальное значение линейная целевая функция z(X) достигает в одной из крайних точек (на *границе* области Ω допустимых решений).	2. Экстремум может достигаться не только на *границе, но и внутри* области Ω допустимых решений.
3. Экстремальное значение z(X) целевой функции является и *глобальным* значением.	3. Целевая функция z(X) в области Ω может иметь *несколько локальных* экстремумов.

На рисунке приводится классификация задач и методов нелинейного программирования.

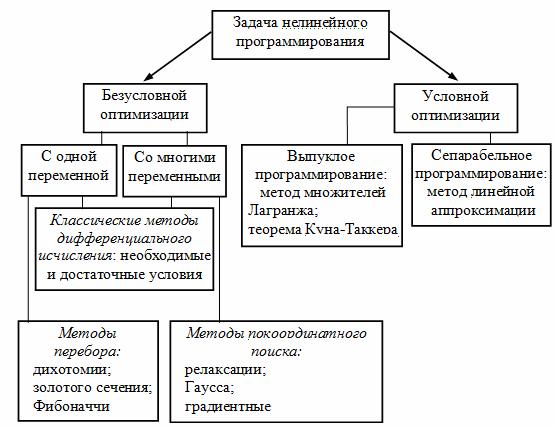
Рисунок - Классификация задач и методов нелинейного программирования

Большинство существующих методов в нелинейном программировании можно разделить на два больших класса:

Прямые методы - методы непосредственного решения исходной задачи. Прямые методы порождают последовательность точек – решений, удовлетворяющих ограничениям, обеспечивающим монотонное убывание целевой функции.
Недостаток: трудно получить свойство глобальной сходимости.
Задачи с ограничениями в виде равенств.
Метод замены переменных (МЗП)
Двойственные методы - методы, использующие понятие двойственности. В этом случае легко получить глобальную сходимость.
Недостаток: не дают решения исходной задачи в ходе решения – оно реализуемо лишь в конце итерационного процесса.
- Метод множителей Лагранжа (ММЛ)
- Методы штрафов
- Метод множителей
- Методы линеаризации для задач условной оптимизации
  Алгоритм Франка–Вульфа
  Метод допустимых направлений Зойтендейка
- Метод условного градиента
- Метод проекции градиента
- Сепарабельное программирование.
- Квадратичное программирование

Методы поиска нулей функции

Методы минимизации функций

Функция одной переменной

Функция двух переменных

Матрица Гессе. 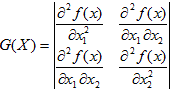. Позволяет ответить на вопрос является ли функция выпуклой или вогнутой, а также определить тип экстремума (минимум или максимум).
Производные второго порядка
Экстремум функции двух переменных.

Методы прямого поиска

Метод Хука–Дживса
Метод сопряженных направлений (метод Пауэлла). Найти минимум целевой функции методом сопряженных направлений: f(x)=3x₁ – x₁³ + 3x₂² + 4x₂. x⁰=(0.78;1)

Градиентные методы

Метод наискорейшего спуска (метод Коши).
Метод Ньютона
Метод Марквардта. Найти минимум функции: y=x₁²+4x₂²+x₁x₂+1-5x₂ методом Марквардта с начальной точкой (10;10) и ε_x=ε_y= ε_|_▽_f(_x)|=0.5. Предельное число итераций равно M=5.
Метод сопряженных градиентов (метод Флетчера-Ривса).
Метод Бройдена–Флетчера–Гольдфарба–Шанно (квазиньютоновские методы).

Нелинейное программирование

Прямые методы

Метод множителей Лагранжа. В задачах 301-320 используя метод множителей Лагранжа найти точки экстремума функции z=f(x,y) при заданном условии: z=xy+7x, 2x+y=1
Условия Куна-Таккера.

Метод проекции градиента.
Метод условного градиента.

Методы линеаризации для задач условной оптимизации

Методы перебора применимы для отыскания экстремумов унимодальных целевых функций. Действие любого из методов поиска заключается в сужении области поиска экстремума (длины _{l 0}):
а) до области заданной длины (_e> 0), проводя минимальное число измерений значений функции (методы дихотомии, золотого сечения);
б) до наименьших возможных размеров _ln при заданном числе измерений n (метод Фибоначчи).
Первая формулировка целесообразна в том случае, если с каждым измерением связаны значительные затраты средств или времени, однако на поиск отпускаются неограниченные средства, которые мы все же стремимся минимизировать; вторая – когда исследователь располагает ограниченными средствами и, зная расходы, связанные с каждым измерением, стремится получить наилучший результат.

Классические методы нахождения экстремумов функций предполагают, что целевые функции непрерывные и гладкие. Для существования точки экстремума должны выполняться необходимые и достаточные условия. Необходимыми условиями существования экстремума являются требования обращения в нуль частных производных первого порядка целевой функции по каждой из переменных. Точка, найденная из необходимых условий, называется стационарной (подозрительной на оптимальную). В качестве стационарных точек могут быть точки перегиба, седловые точки и др. Поэтому необходим учет достаточных условий нахождения экстремумов функций. Он сложен для функций многих переменных как в алгебраическом, так и в вычислительном плане. Так в случае функции двух переменных достаточным условием существования экстремума будет положительная определенность матрицы А размером 2x2 (условие Лежандра-Клебша), составленной из вторых частных производных функции. Недостатком классического метода дифференциального исчисления является и то, что он дает возможность найти экстремум только в том случае, если он лежит внутри области определения функции. Если экстремум находится на границе области определения, то этот метод становится бессильным.

Методы покоординатного спуска относятся к группе приближенных методов нелинейной оптимизации и направлены на уменьшение трудностей, связанных с отысканием экстремума функции цели со сложной аналитической структурой классическими методами дифференциального исчисления. Суть этих методов заключается в продвижении от исходной точки в области определения функции к точке оптимума итеративно; в методе Гаусса – последовательно по каждой из переменных (покоординатно); в градиентных методах – одновременно по всем переменным в направлении градиента или антиградиента.

Критерием окончания итеративных процедур является равенство нулю всех частных производных целевой функции, или квадрат суммы всех частных производных целевой функции должен быть не более заданного числа _e, или разность достигнутого значения целевой функции и значения в предыдущей точке должна быть не более _e и другие.