Метод деления отрезка пополам
Метод Фибоначчи
Этот алгоритм используется для нахождения минимума функции. Если необходимо найти нули функции, то используется другой алгоритм.
1)
10•x•e2x записываем как: 10*x*exp(2*x)
2)
x•e-x+cos(3x) ≡ x*exp(-x)+cos(3*x)
3)
x3-x2+3 ≡ x^3-x^2+3
Рассмотрим последовательный поиск точки xф ∈ [0;1], в которой унимодальная на отрезке [0,1] функция f(x) достигает наименьшего значения f0=f(x0).
Метод прямого поиска, основанный на делении пополам отрезка, на котором находится точка x0, называют методом дихотомии.
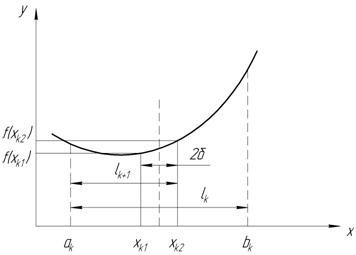
Рис.1
Алгоритм метода дихотомии
Пусть известно, что на k-м шаге последовательного поиска xф ∈ [ak;bk] ⊂ [0;1] (на первом шаге при k=1 имеем a1=0 и b1=1). На отрезке [ak, bk] длиной lk выберем две точки xk1=(ak+bk)/2-δ и xk2=(ak+bk)/2+δ (рис. 1), где δ>0 — некоторое достаточно малое число. Вычислим значения f(xk1) и f(xk2) функции f(x) в этих точках и выполним процедуру исключения отрезка.Если f(xk1) < f(xk2), то в силу унимодальности функции f(x) имеем xф ∈ [ak;xk2], а отрезок [xk2,bk] исключаем из дальнейшего рассмотрения.
Наоборот, если f(xk1) ≥f(xk2), то xф ∈ [xk1;bk], а отрезок [ak,xk1] не рассматриваем. В результате получим новый отрезок [ak+l;bk+l] ⊂ [ak;bk].
Если длина lk+1 нового отрезка больше заданной наибольшей допустимой длины ε0интервала неопределенности, то алгоритм метода дихотомии переходит к (k+1)-му шагу, повторяя все описанные для k-го шага действия. Если же lk≤ε0, то вычисления прекращают и полагают x0=(ak+1+bk+1)/2.
Так как lk+1=lk/2+δ или lk+1-2δ =(lk-2δ)/2, то
.
Из этого равенства выводим следующую формулу длины lk отрезка [ak,bk], получаемого на k-м шаге метода дихотомии:
. (1)
Из (1) следует, что lk+1→2δ при k→∞, но при этом lk+1>2δ. Поэтому выполнение неравенства lk+1<ε0, означающее достижение заданной точности нахождения точки xф, возможно лишь при условии выбора 2δ<ε0. Кроме того, нужно учитывать неизбежную погрешность, возникающую при вычислении приближенных значений
функции f(x). Это приводит к дополнительной погрешности ∆0 при нахождении точки x0 (см. 2). Поэтому выбор значения δ ограничен и снизу, т.е.
∆0< 2δ<ε0. (2)
Если эти неравенства нарушаются, то знак разности
может не совпадать со знаком разности f(xk1)-f(xk2), что приводит к ошибочному выполнению процедуры исключения отрезка.
Итак, метод дихотомии — это последовательное построение на каждом k-м шаге поиска точек xk1=(ak+bk)/2-δ и xk2=(ak+bk)/2+δ, симметричных относительно середины отрезка [ak,bk] длины lk. После выполнения k-го шага будет выделен отрезок [ak+1,bk+1] длины lk+1 и вычислено N=2k значений функции. Используя формулу (1) для длины отрезка (интервала неопределенности) и полагая l1=1, получаем
. (3)
Отметим, что после исключения отрезка на k-м шаге описанного алгоритма точки xk1 и xk2 принадлежат новому отрезку [ak+1,bk+1], причем одна из них является внутренней для этого отрезка. Но вычисленное в этой точке значение функции f(x) в методе дихотомии не используют для исключения отрезка на следующем шаге, а проводят вычисления в двух новых точках. Существуют методы последовательного поиска, в которых на каждом k-м шаге начиная с k=2 вычисляют лишь одно новое значение функции в точке, принадлежащей отрезку [ak+1,bk+1]. Это значение вместе с уже вычисленным на предыдущем шаге значением функции во внутренней точке отрезка [ak,bk] используют при выполнении процедуры исключения отрезка на следующем шаге последовательного поиска.
Пример. Пользуясь методом дихотомии (методом одномерного поиска), минимизировать следующую функцию с точностью до одного знака после запятой: f(x)=3x4+(x-1)2
Решение.
x = (0+4)/2 = 2
Шаг приращения δ=0.1
Положим a1 = a, b1 = b. Вычислим x11=x-δ=2-0.1=1.9, x12=x+δ=2+0.1=2.1.
Вычислим f(x11) = 39.9063, f(x12) = 59.5543
Итерация №1.
Поскольку f(x11) < f(x12), то b2 = 2.1, a2 = a1, x22 = 1.9
f(x21) = 2.446, f(x22) = 39.9063
Итерация №2.
Поскольку f(x21) < f(x22), то b3 = 1.9, a3 = a2, x32 = 0.95
f(x31) = 1.5885, f(x32) = 2.446
Итерация №3.
Поскольку f(x31) < f(x32), то b4 = 0.95, a4 = a3, x42 = 0.85
f(x41) = 0.45, f(x42) = 1.5885
Итерация №4.
Поскольку f(x41) < f(x42), то b5 = 0.85, a5 = a4, x52 = 0.375
f(x51) = 0.4891, f(x52) = 0.45
Остальные расчеты сведем в таблицу.
| N | an | bn | bn-an | xn1 | xn2 | F(xn1) | F(xn2) |
| 1 | 0 | 4 | 2 | 1.9 | 2.1 | 39.9063 | 59.5543 |
| 2 | 0 | 2.1 | 2.1 | 0.95 | 1.9 | 2.446 | 39.9063 |
| 3 | 0 | 1.9 | 1.9 | 0.85 | 0.95 | 1.5885 | 2.446 |
| 4 | 0 | 0.95 | 0.95 | 0.375 | 0.85 | 0.45 | 1.5885 |
| 5 | 0 | 0.85 | 0.85 | 0.325 | 0.375 | 0.4891 | 0.45 |
| 6 | 0.325 | 0.85 | 0.525 | 0.375 | 0.6875 | 0.45 | 0.7679 |
| 7 | 0.325 | 0.6875 | 0.3625 | 0.4063 | 0.375 | 0.4343 | 0.45 |
| 8 | 0.325 | 0.375 | 0.05 | 0.25 | 0.4063 | 0.5742 | 0.4343 |
Ответ: x = 0.35; F(x) = 0.46751875