Алгоритм метода половинного деления (метод дихотомии)
Метод деления пополам позволяет исключать в точности половину интервала на каждой итерации. При использовании метода считается, что функция непрерывна и имеет на концах интервала разный знак. После вычисления значения функции в середине интервала одна часть интервала отбрасывается так, чтобы функция имела разный знак на концах оставшейся части. Итерации метода деления пополам прекращаются, если интервал становится достаточно малым.Словесный алгоритм.
- Найдем отрезок [a,b]: f(a)f(b)<0.
- Положим c=(a+b)/2.
- Если f(a)f(c)<0, то положим b=c, в противном случае a=c.
- Если
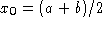, то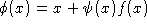 
, в противном случае выполнить пункт 2.
a - левая граница
b - правая граница
sigma - погрешность
max_step - максимальное кол-во шагов
x - найденный корень
f_a – значение функции в начале интервала
f_b – значение функции в конце интервала
xm – середина интервала
f_xm – значение функции в середине интервала
k – переменная цикла
Блок – схема алгоритма
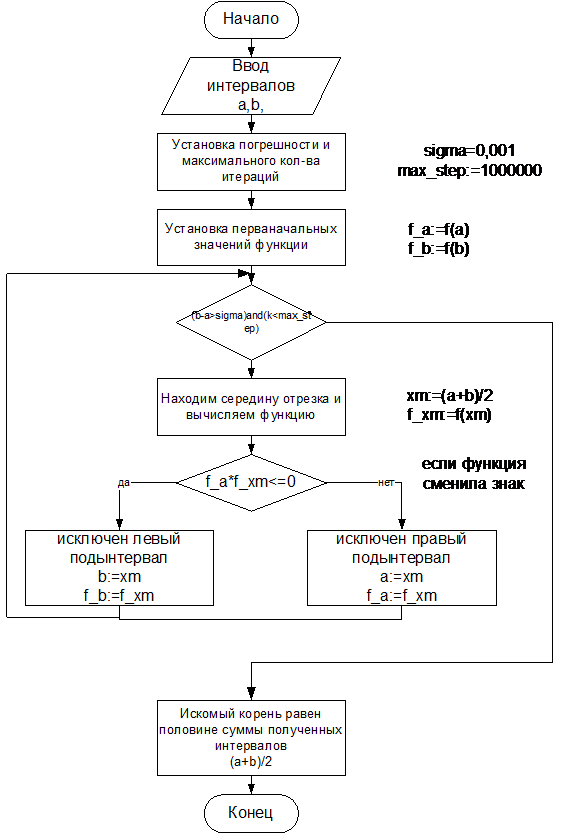
Метод половинного деления на языке Pascal. Листинг
program dohometr;
var
a:real; {левая граница}
b:real; {правая граница}
sigma:real; {погрешность}
max_step:longint; {максимальное кол-во шагов}
x:real; {найденный корень}
function f(x:real):real;{функция}
begin
f:=x*sin(x);
end;
function FindKoren(a,b:real):real;{уменьшение интервала неопределенности}
var f_a,f_b,xm,f_xm:real;k:longint;
begin
k:=0;
f_a:=f(a); {устанавливаем первоначальное значение}
f_b:=f(b); {устанавливаем первоначальное значение}
while (b-a > sigma)and(k < max_step) do
begin
xm:=(a+b)/2; {середина интервала}
f_xm:=f(xm);
if (f_a*f_xm <=0) then {функция должна иметь разный знак}
begin {на границах интервала}
b:=xm;
f_b:=f_xm {исключен левый подынтервал}
end
else
begin
a:=xm;
f_a:=f_xm; {исключен правый подынтервал}
end;
end;
findkoren:=(a+b)/2; {ответ}
end;
begin
Write('Введите левый интервал, a = ');ReadLN(a);
Write('Введите правый интервал, b = ');ReadLN(b);
sigma:=0.001; {погрешность}
max_step:=1000000;
WriteLN('Корень равен, х = ',FindKoren(a,b):10:3);
end.
Метод дихотомии в Excel
Чтобы найти корни уравнения с помощью метода половинного деления (он же метод дихотомии - деление отрезка пополам) необходимо:- Получить шаблон через сервис.
- Уточнить интервалов в ячейках
B2,B3. - Копировать строки итераций до требуемой точности.
В ячейку B2 заносим начало интервала a, в ячейку B3 заносим конец интервала b. Строку 4 отводим под заголовок таблицы. Сам процесс итераций организуем в ячейках A5:G5.
Пример решения
Найти корни уравнения: x•sin(x) = 0
Чтобы отыскать предварительные интервалы, строим график функции.
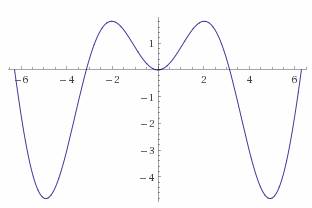
Как видно, первый корень лежит в интервале [-2;2], второй корень функции находится в интервале [2;4].
Уточним интервалы, в которых будут находиться корни уравнения. Для этого исходный интервал [2;4] разобьем на 10 подынтервалов.
h5 = 2 + 5*(4-2)/10 = 3
h6 = 2 + (5+1)*(4-2)/10 = 3.2
Поскольку F(3)*F(3.2)<0, то корень лежит в пределах [3;3.2].
Итерация 1.
Находим середину отрезка: c = (3 + 3.2)/2 = 3.1
F(c) = 0.13
F(x) = 0.42
Поскольку F(c)•F(x) > 0, то a=3.1
Итерация 2.
Находим середину отрезка: c = (3.1 + 3.2)/2 = 3.15
F(c) = -0.0265
F(x) = 0.13
Поскольку F(c)•F(x) < 0, то b=3.15
Итерация 3.
Находим середину отрезка: c = (3.1 + 3.15)/2 = 3.13
F(c) = 0.0518
F(x) = 0.13
Поскольку F(c)•F(x) > 0, то a=3.13
Итерация 4.
Находим середину отрезка: c = (3.13 + 3.15)/2 = 3.14
F(c) = 0.0128
F(x) = 0.0518
Поскольку F(c)•F(x) > 0, то a=3.14
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 3.1 | 3 | 3.2 | 0.1289 | 0.1289 |
| 2 | 3.15 | 3.1 | 3.2 | 0.1289 | -0.02648 |
| 3 | 3.125 | 3.1 | 3.15 | 0.05185 | 0.05185 |
| 4 | 3.1375 | 3.125 | 3.15 | 0.01284 | 0.01284 |
| 5 | 3.1438 | 3.1375 | 3.15 | 0.01284 | -0.00678 |
| 6 | 3.1406 | 3.1375 | 3.1438 | 0.00304 | 0.00304 |
| 7 | 3.1422 | 3.1406 | 3.1438 | 0.00304 | -0.00187 |
| 8 | 3.1414 | 3.1406 | 3.1422 | 0.000586 | 0.000586 |
Количество итераций, N = 8
Параметр сходимости.
