Метод половинного деления (метод дихотомии или метод бисекции)

Оглавление

• Онлайн калькулятор
• Алгоритм метода половинного деления (метод дихотомии)
• Метод половинного деления на языке Pascal
• Метод половинного деления в Excel
• Примеры решений

Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξ_i являющихся приближением корня на i-ом шаге.
ξ_i=½(b_i+a_i), i=0,1,...
где a₀=a; b₀=b; a_i;b_i - границы подынтервалов, в которых f(a_i)f(b_i)<0. Рассмотрим разности
|ξ₁- ξ₀|, |ξ₂- ξ₁|, …, |ξ_n- ξ_n-1|.
Имеем |ξ₁-ξ₀|=½(b₁+a₁-b₀-a₀). Так как всегда имеем либо b₁=b₀, a₁=½(b₀+a₀), либо a₁=a₀, b₁=½(a₀+b₀), поэтому 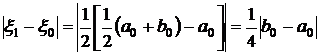 , если, b₁=b₀
 либо 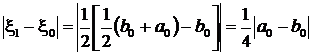, если a₁=a₀.
Повторяя аналогичные рассуждения и учитывая, что всегда выполняется соотношение либо b_i=b_i-1, a_i=½(b_i-1+a_i-1), либо b_i=½(b_i-1+a_i-1), a_i=a_i-1. Получим
;
;
, где a₀=a, b₀=b.
Отсюда видно, что какое бы малое число ε>0 мы ни задали, всегда можно найти такое n, что  ч.т.д.
Графически метод дихотомии выглядит следующим образом

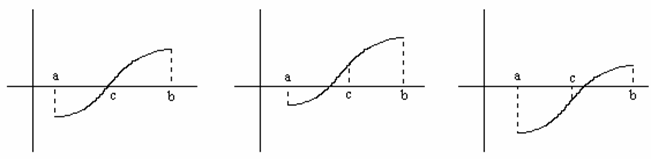
|f(c)|≤δ f(a)f(c)<0 f(b)f(c)<0

Сходимость метода дихотомии линейная с коэффициентом α=0,5. Покажем это.
Если в качестве x_n брать a_n, то из формулы (6) мы можем записать , . Отсюда следует .
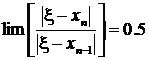Отметим, что за 10 итераций (n=10) интервал уменьшается в 2¹⁰ = 1024 ≈ 10³ раз. За 20 итераций (n=2) уменьшается в 2²⁰ ≈ 10⁶ раз.

Перейти к онлайн решению своей задачи

Скачать решение

Методом дихотомии также можно находить и минимальное и максимальное значения функции. Для этого необходимо найти производную функции и приравнять ее нулю.

Алгоритм метода половинного деления (метод дихотомии)

1. Найдем отрезок [a,b]: f(a)f(b)<0.
2. Положим c=(a+b)/2.
3. Если f(a)f(c)<0, то положим b=c, в противном случае a=c.
4. Если , то , в противном случае выполнить пункт 2.

Блок – схема алгоритма

Метод половинного деления на языке Pascal. Листинг

program dohometr;
var
a:real;		{левая граница}
b:real;		{правая граница}
sigma:real;	{погрешность}
max_step:longint;	{максимальное кол-во шагов}
x:real;		{найденный корень}

function f(x:real):real;{функция}
begin
f:=x*sin(x);
end;

function FindKoren(a,b:real):real;{уменьшение интервала неопределенности} 
var f_a,f_b,xm,f_xm:real;k:longint;
begin
k:=0;
f_a:=f(a);	       {устанавливаем первоначальное значение}
f_b:=f(b);	       {устанавливаем первоначальное значение}
while (b-a > sigma)and(k < max_step) do
		begin
		xm:=(a+b)/2;	          {середина интервала}
		f_xm:=f(xm);
if (f_a*f_xm <=0) then       {функция должна иметь разный знак}
			begin	          {на границах интервала}
			b:=xm;
			f_b:=f_xm	          {исключен левый подынтервал}
			end
			else
			begin
			a:=xm;
			f_a:=f_xm;	    {исключен правый подынтервал}
			end;
	end;
findkoren:=(a+b)/2;	    {ответ}
end;

begin
Write('Введите левый интервал, a = ');ReadLN(a);
Write('Введите правый интервал, b = ');ReadLN(b); 
sigma:=0.001;         {погрешность} 
max_step:=1000000;
WriteLN('Корень равен, х = ',FindKoren(a,b):10:3); 
end.

Метод дихотомии в Excel

1. Получить шаблон через сервис.
2. Уточнить интервалов в ячейках B2, B3.
3. Копировать строки итераций до требуемой точности.

В ячейку B2 заносим начало интервала a, в ячейку B3 заносим конец интервала b. Строку 4 отводим под заголовок таблицы. Сам процесс итераций организуем в ячейках A5:G5.

Пример решения

Решение. Чтобы отыскать предварительные интервалы, строим график функции.

Видеоотчет

Как видно, первый корень лежит в интервале [-2;2], второй корень функции находится в интервале [2;4].
Уточним интервалы, в которых будут находиться корни уравнения. Для этого исходный интервал [2;4] разобьем на 10 подынтервалов.
h₅ = 2 + 5*(4-2)/10 = 3
h₆ = 2 + (5+1)*(4-2)/10 = 3.2
Поскольку F(3)*F(3.2)<0, то корень лежит в пределах [3;3.2].
Итерация 1.
Находим середину отрезка: c = (3 + 3.2)/2 = 3.1
F(c) = 0.13
F(x) = 0.42
Поскольку F(c)•F(x) > 0, то a=3.1
Итерация 2.
Находим середину отрезка: c = (3.1 + 3.2)/2 = 3.15
F(c) = -0.0265
F(x) = 0.13
Поскольку F(c)•F(x) < 0, то b=3.15
Итерация 3.
Находим середину отрезка: c = (3.1 + 3.15)/2 = 3.13
F(c) = 0.0518
F(x) = 0.13
Поскольку F(c)•F(x) > 0, то a=3.13
Итерация 4.
Находим середину отрезка: c = (3.13 + 3.15)/2 = 3.14
F(c) = 0.0128
F(x) = 0.0518
Поскольку F(c)•F(x) > 0, то a=3.14
Остальные расчеты сведем в таблицу.

Пример №1. Найти экстремум функции: y=5x²-4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].
Решение. Находим производную функции: y ' = 10x-4. Найдем нули функции методом дихотомии: y'=0.
Поскольку F(0)*F(10)<0 (т.е. значения функции на его концах имеют противоположные знаки), то корень лежит в пределах [0;10].
Итерация 1.
Находим середину отрезка: c = (0 + 10)/2 = 5
F(x) = 46
F(c) = -4
Поскольку F(c)•F(a) < 0, то b=5
Итерация 2.
Находим середину отрезка: c = (0 + 5)/2 = 2.5
F(x) = 21
F(c) = 46
Поскольку F(c)•F(a) < 0, то b=2.5
Итерация 3.
Находим середину отрезка: c = (0 + 2.5)/2 = 1.25
F(x) = 8.5
F(c) = 21
Поскольку F(c)•F(a) < 0, то b=1.25
Итерация 4.
Находим середину отрезка: c = (0 + 1.25)/2 = 0.625
F(x) = 2.25
F(c) = 8.5
Поскольку F(c)•F(a) < 0, то b=0.625
Видеоотчет
Остальные расчеты сведем в таблицу.

На отрезке [0,10] функция имеет экстремум x=0.3906.

Пример №2. Методом дихотомического поиска найдите максимумы функций, пологая, что Δ=0,05.
f(x) = x*cos(x), 0 ≤x≤ π

Пример №3. Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10^-2. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10^-4. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x² = 10, a = 2.6, b = 3

Найдем корни уравнения: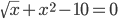
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b)<0. Метод дихотомии заключается в следующем.
Определяем половину отрезка c=¹/₂(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| < ε, то c – корень. Здесь ε - заданная точность.
2. Если f(c)f(a)<0, то корень лежит в интервале [a,c].
3. Если f(c)f(b)<0, то корень лежит на отрезке[c,b].
Продолжая процесс половинного деления в выбранных подынтервалов, можно дойти до сколь угодно малого отрезка, содержащего корень ξ.
Так как за каждую итерацию интервал, где расположен корень уменьшается в два раза, то через n итераций интервал будет равен:
b_n-a_n=¹/₂ⁿ(b-a)
В качестве корня ξ. возьмем ¹/₂(a_n+b_n). Тогда погрешность определения корня будет равна (b_n – a_n)/2. Если выполняется условие:
(b_n – a_n)/2 < ε
то процесс поиска заканчивается и ξ = ¹/₂(a_n+b_n).
Решение.
Поскольку F(2.6)*F(3)<0, то корень лежит в пределах [2.6;3].
Итерация 1.
Находим середину отрезка: c = (2.6 + 3)/2 = 2.8
F(x) = -0.487
F(c) = -1.628
Поскольку F(c)•F(x) > 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) < 0, то b=2.9
Итерация 3.
Находим середину отрезка: c = (2.8 + 2.9)/2 = 2.85
F(x) = -0.189
F(c) = 0.113
Поскольку F(c)•F(x) < 0, то b=2.85
Итерация 4.
Находим середину отрезка: c = (2.8 + 2.85)/2 = 2.825
F(x) = -0.339
F(c) = -0.189
Поскольку F(c)•F(x) > 0, то a=2.825
Остальные расчеты сведем в таблицу.

Пример №2. Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε₁ = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации  с точностью ε₂ = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε₂ число итераций.