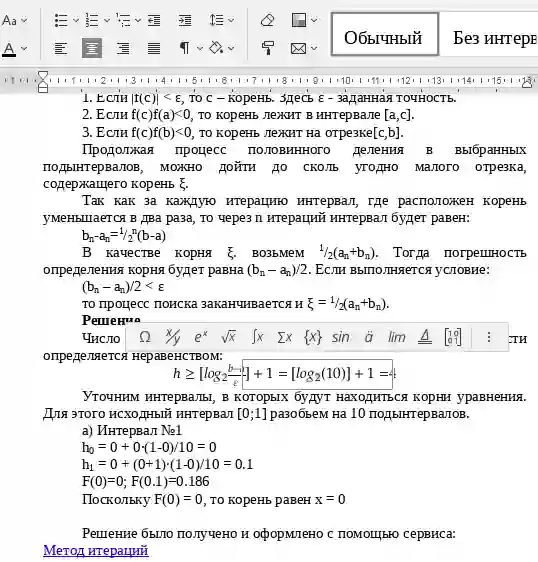
Метод итераций
Назначение сервиса. Онлайн-калькулятор предназначен для отыскания корней уравнения методом итераций.Правила ввода функции
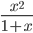≡ x^2/(1+x)
cos2(2x+π) ≡ (cos(2*x+pi))^2
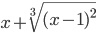≡ x+(x-1)^(2/3)
Заменим его равносильным уравнением
Выберем начальное приближение корня x0 и подставим его в правую часть уравнения (1). Тогда получим некоторое число
Подставляя теперь в правую часть (2) вместо x0 число x1 получим число x2=φ(x1). Повторяя этот процесс, будем иметь последовательность чисел
Если эта последовательность сходящаяся, то есть существует предел
, то переходя к пределу в равенстве (3) и предполагая функцию φ(x) непрерывной найдем
Таким образом, предел ξ является корнем уравнения (1) и может быть вычислен по формуле (3) с любой степенью точности.
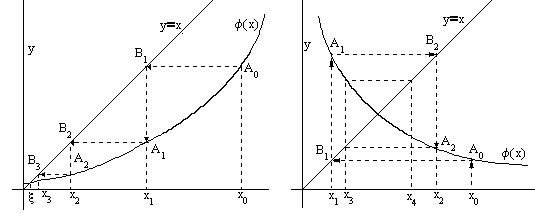
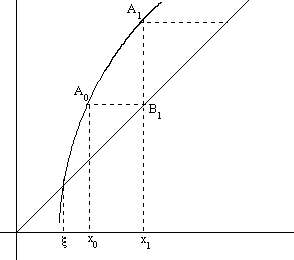
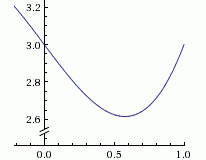
Рис. 2. |φ′(x)|>1 - расходящийся процесс
На рис.1а, 1б в окрестности корня |φ′(x)|<1 и процесс итерации сходится. Однако, если рассмотреть случай |φ′(x)|>1, то процесс итерации может быть расходящимся (см. рис.2).
Достаточные условия сходимости метода итерации
Теорема 7. Пусть функция φ(x) определена и дифференцируема на отрезке [a,b], причем все ее значения φ(x)∈[a,b] и пусть |φ′(x)|≤q<1 при x∈[a,b]. Тогда процесс итерации xn = φ(xn-1) сходится независимо от начального значения x0∈[a,b] и предельное значение
является единственным корнем уравнения x= φ(x) на отрезке [a,b].
Доказательство: Рассмотрим два последовательных приближения xn = φ(xn-1) и xn+1= φ(xn) и возьмем их разность xn+1-xn=φ(xn)-φ(xn-1). По теореме Лагранжа правая часть может быть представлена как
Тогда получим
Полагая n=1,2,...
|x3-x2|≤q|x2-x1|≤q²|x1-x0|
|xn+1-xn≤qn|x1-x0| (4)
Из (4) в силу условия q<1 видно, что последовательность {xn} сходится к некоторому числу ξ, то есть
, и следовательно,
(в силу непрерывности функции φ(x))
или
ξ= φ(ξ) ч.т.д.
Для погрешности корня ξ можно получить следующую формулу.
Имеем xn=φ(xn-1).
Далее ξ-xn=ξ-φ(xn-1) = φ(ξ)-φ(xn-1) →
Теперь φ(xn-1)=φ(xn)-φ′(c)(xn-xn-1) →
φ(ξ)-φ(xn)+φ′(c)(xn-xn-1)
В результате получим
или
|ξ-xn|≤q|ξ-xn|+q|xn-xn-1|
Отсюда
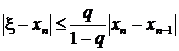, (5)откуда видно, что при q близком к 1 разность |ξ -xn| может быть очень большой несмотря на то что |xn-xn-1|<ε, где ε-заданная величина. Для того, чтобы вычислить ξ с точностью ε необходимо обеспечить
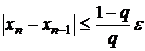. (6)Тогда подставляя (6) в (5), получим |ξ -xn|<ε.
Если q очень мало, то вместо (6) можно использовать
Сходимость метода итерации линейная с коэффициентом сходимости α=q. Действительно, имеем
ξ-xn=φ(ξ)-φn-1 = φ′(c)·(ξ-xn-1), отсюда |ξ-xn|≤q·|ξ-xn-1|.
Замечание. Пусть в некоторой окрестности корня ξ∈(a,b) уравнения x= φ(x) производная φ’(x) сохраняет постоянный знак и выполнено неравенство |φ’(x)|≤q<1. Тогда, если φ’(x) положительна, то последовательные приближения xn = φ(xn-1) сходятся к корню монотонно.
Если же φ’(x) отрицательна, то последовательные приближения колеблются около корня.
Рассмотрим способ представления уравнения f(x)=0 в форме x= φ(x).
Функцию φ(x) необходимо задать такую, чтобы |φ’(x)| была малой величиной в окрестности корня.
Пусть известно m1 и M1 - наименьшее и наибольшее значения производной f’(x)
0<m1≤f’(x) ≤M1 (7)
Заменим уравнение f(x)=0 эквивалентным ему уравнением
x = x - λf(x).
Положим φ(x) = x- λf(x). Подберем параметр λ таким образом, чтобы в окрестности корня ξ выполнялось неравенство
Отсюда на основании (7) получаем
Тогда выбирая λ = 1/M1, получим
q = 1-m1/M1 < 1.
Если λ =1/f’(x), то итерационная формула xn = φ(xn-1) переходит в формулу Ньютона
Метод итераций в Excel
В ячейкуB2 заносим начало интервала a, в ячейку B3 заносим конец интервала b. Строку 4 отводим под заголовок таблицы. Сам процесс итераций организуем в ячейках A5:D5.
Процесс нахождения нулей функции методом итераций состоит из следующих этапов:
- Получить шаблон с омощью этого сервиса.
- Уточнить интервалы в ячейках
B2,B3. - Копировать строки итераций до требуемой точности (столбец
D).
A - номер итерации, столбец B - корень уравнения X, столбец C - значение функции F(X), столбец D - точность eps.
Пример. Найти корень уравнения e-x-x=0, x=∈[0,1], ε=0.001 (8)
Решение.
Представим уравнение (8) в форме x=x-λ(e-x-x)
Найдем максимальное значение производной от функции f(x)= e-x-x.
max f′(x)=max(-(e-x+1)) ≈ -1.37. Значение 
. Таким образом, решаем следующее уравнение
x=x+0,73(e-x-x)
Значения последовательных приближений даны в таблице.
| n | xi | f(xi) |
| 1 | 0.0 | 1.0 |
| 2 | 0.73 | -0.2481 |
| 3 | 0.5489 | 0.0287 |
| 4 | 0.5698 | -0.0042 |
| 5 | 0.5668 | 0.0006 |