Функция Лагранжа
Функция Лагранжа - функция L(X,λ), определенная выражением L(X,λ) = F(X) + ∑λiφi(x), где λi - множители Лагранжа. Функция Лагранжа используется при решении задач на условный экстремум.Назначение сервиса. Онлайн-калькулятор используется для нахождения экстремума функции через множители Лагранжа в онлайн режиме (см. пример и пример решения графическим способом). При этом решаются следующие задачи:
- составляется функция Лагранжа L(X) в виде линейной комбинации функции F(X) и ограничений gi(x);
- находятся частные производные функции Лагранжа, ∂L/∂xi, ∂L/∂λi;
- составляется система из (n + m) уравнений, ∂L/∂xi = 0.
- определяются переменные xi и множители Лагранжа λi.
Метод множителей Лагранжа применяется как в линейном программировании, так и в нелинейном. В экономике этот метод используется в задаче потребительского выбора.
Правило множителей Лагранжа
Если x*=(x1,..., xn) - решение задачи на условный экстремум, то существует хотя бы одна ненулевая система множителей Лагранжа λ*(λ1,...,λm) такая, что точка (x*) является точкой стационарности функции Лагранжа по переменным xj и λi, рассматриваемым, как независимые переменные.Метод множителей Лагранжа заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — функции Лагранжа.
Пример 1. Методом множителей Лагранжа решить следующую задачу оптимизации:
min f(x) = x12 + x22
h1(x) = 2x1 + x2 -2 = 0
Соответствующая задача оптимизации без ограничений записывается в следующем виде:
L(x, λ) = x12 + x22 + λ(2x1 + x2 – 2) → min
Решение:
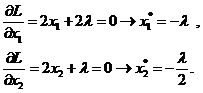
Для того чтобы проверить, соответствует ли стационарная точка X минимуму, вычислим матрицу Гессе функции L(x, λ), рассматриваемой как функция от x,
![]() ,
,
которая оказывается положительно определенной (2*2 – 0*0 = 4 > 0).
Это означает, что L(x, λ) – выпуклая функция. Следовательно, координаты x* = (-λ, λ/2) определяют точку глобального минимума. Оптимальное значение λ находится путем подстановки значений x1* иx2*в уравнение ограничений 2x1 + x2 -2 = 0,откуда вычисляем значение λ:
2λ + λ/2 = -2, откуда λ = -0.8
Таким образом, минимум достигается в точке x* с координатами x1* = 0.8 и x2* = 0.4. Значение ЦФ:
min f(x) = 0.8
Ответ: x*= [0.8; 0.4]T , f(x*) = 0.8
Пример 2. Исследовать на условный экстремум функцию f(x,y)max = x2 + 8xy+3y2 при данных уравнениях связи.
9x +10y = 29