Метод множителей Лагранжа. Пример решения
Пример №1. Имеется два способа производства некоторого продукта. Издержки производства при каждом способе зависят от произведенных x1 и у2 следующим образом: g(x1)= 9x1 + x12, g(x2)=6x2 + x22 . За месяц необходимо произвести 3×50 единиц продукции, распределив ее между двумя способами так, чтобы минимизировать общие издержки.Решение. Найдем экстремум функции F(X)=9·x1+x12+6·x2+x22, используя сервис функция Лагранжа
:
L(X, λ)=F(X)+∑λi·φi(X)
где F(X) - целевая функция вектора X, φi(X) - ограничения в неявном виде (i=1..n)
В качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция:
F(X) = 9·x1+x12+6·x2+x22
Перепишем ограничение задачи в неявном виде: φi(X)= x1+x2-150=0
Составим вспомогательную функцию Лагранжа: L(X, λ) = 9·x1+x12+6·x2+x22 + λ(x1+x2-150)
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенному множителю λ.
Составим систему:
∂L/∂x1 = 2·x1+λ+9 = 0
∂L/∂x2 = λ+2·x2+6 = 0
∂F/∂λ = x1+x2 -150= 0
Систему решаем с помощью метода Гаусса или используя формулы Крамера.
Запишем систему в виде:
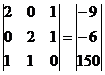
Для удобства вычислений поменяем строки местами:
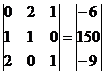
Добавим 2-ую строку к 1-ой:
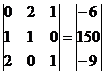
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
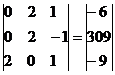
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
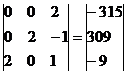
Из 1-ой строки выражаем x3
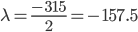
Из 2-ой строки выражаем x2
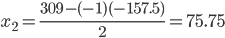
Из 3-ой строки выражаем x1
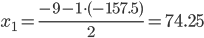
Таким образом, чтобы общие издержки производства были минимальны, необходимо производить x1 = 74.25; x2 = 75.75.
Задание. По плану производства продукции предприятию необходимо изготовить 50 изделий. Эти изделия могут быть изготовлены 2-мя технологическими способами. При производстве x1 - изделий 1-ым способом затраты равны 3x1+x12 (т. руб.), а при изготовлении x2 - изделий 2-ым способом они составят 5x2+x22 (т. руб.). Определить сколько изделий каждым из способов необходимо изготовить, чтобы общие затраты на производство были минимальные.
Решение: составляем целевую функцию и ограничения:
F(X) = 3x1+x12 + 5x2+x22 → min
x1+x2 = 50
Пример №2. В качестве целевой функции, подлежащей оптимизации, выступает функция: F(X) = x1·x2
при условии: 3x1 + x2 = 6.
Перепишем ограничение задачи в неявном виде: φi(X)=3x1 + x2 - 6 = 0
Составим вспомогательную функцию Лагранжа: L(X, λ)=x1·x2+λ(3x1 + x2 - 6)
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенному множителю λ.
Составим систему:
∂L/∂x1 = 3·λ+x2 = 0
∂L/∂x2 = x1+λ = 0
∂F/∂λ = 3·x1 + x2-6 = 0
Решаем данную систему методом Гаусса.
Запишем систему в виде:
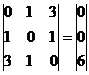
Добавим 2-ую строку к 1-ой:
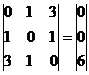
Умножим 2-ую строку на (3). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
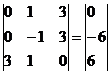
Добавим 2-ую строку к 1-ой:
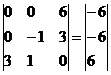
Из 1-ой строки выражаем x3
![]()
Из 2-ой строки выражаем x2
![]()
Из 3-ой строки выражаем x1
![]()
Точка экстремума (1;3). Значение функции в точке экстремума F(1;3)=3.
Пример №3. Рассмотрим функцию: F(X)=3·x12+2·x22-3·x1+1
и условия-ограничения: x12 + x22 = 4
L(X, λ)=3·x12+2·x22-3·x1+1 + λ(x12 + x22 - 4)
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенному множителю λ.
Составим систему:
∂L/∂x1 = 2·x1·(λ+3)-3 = 0
∂L/∂x2 = 2·(λ+2)·x2 = 0
∂F/∂λ = x12+x22-4 = 0
Выражаем из первого уравнения x1:
![]()
Из второго уравнения получаем x2 = 0.
Подставляем в третье уравнение:
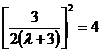 или
или ![]()
Перепишем в виде: λ+3 =3/4 откуда λ=-9/4.
Подставляя λ в выражение для x1, получаем:
![]()
Стационарная точка (2;0). Значение функции в стационарной точке: F(2;0) = 7.
Пример №4. Найдем локальные стационарные точки функции:
F(X) = 3·x1·x2
g(x): 2·x1+x2=3
Перепишем ограничение задачи в неявном виде: 2·x1+x2-3 = 0
Составим вспомогательную функцию Лагранжа:
L = 3·x1·x2 + λ·(2·x1+x2-3)
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенному множителю λ.
Составим систему:
∂L/∂x1 = 2·λ+3·x2 = 0
∂L/∂x2 = 3·x1+λ = 0
∂F/∂λ = 2·x1+x2-3 = 0
Данную систему решаем методом обратной матрицы:
Запишем матрицу в виде: 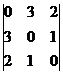
Вектор B: BT = (0,0,3)
Главный определить: ∆ = 0·(0·0-1·1)-3·(3·0-1·2)+2·(3·1-0·2) = 12
Транспонированная матрица: 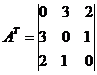
Алгебраические дополнения
![]() ; ∆1,1 = (0·0-1·1) = -1
; ∆1,1 = (0·0-1·1) = -1
![]() ; ∆1,2 = -(3·0-2·1) = 2
; ∆1,2 = -(3·0-2·1) = 2
![]() ; ∆1,3 = (3·1-2·0) = 3
; ∆1,3 = (3·1-2·0) = 3
![]() ; ∆2,1 = -(3·0-1·2) = 2
; ∆2,1 = -(3·0-1·2) = 2
![]() ; ∆2,2 = (0·0-2·2) = -4
; ∆2,2 = (0·0-2·2) = -4
![]() ; ∆2,3 = -(0·1-2·3) = 6
; ∆2,3 = -(0·1-2·3) = 6
![]() ; ∆3,1 = (3·1-0·2) = 3
; ∆3,1 = (3·1-0·2) = 3
![]() ; ∆3,2 = -(0·1-3·2) = 6
; ∆3,2 = -(0·1-3·2) = 6
![]() ; ∆3,3 = (0·0-3·3) = -9
; ∆3,3 = (0·0-3·3) = -9
Обратная матрица: 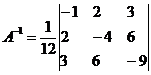
Вектор результатов X: X = A-1·B
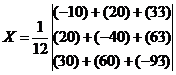
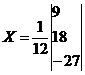
x1 = 9 / 12 = 0.75
x2 = 18 / 12 = 1.5
λ = -27 / 12 = -2.25
Таким образом, локальный экстремум (0.75; 1.5). Значение функции в стационарной точке F(0.75; 1.5) = 3.375.
Пример №5. Найдем точку экстремума функции:
F(X) = 2x12+x1x2+x22+2x1-4x2
Перепишем ограничение задачи в неявном виде:
φ1 = x1+x2-2 = 0
Составим вспомогательную функцию Лагранжа:
L = 2x12+x1x2+x22+2x1-4x2 + λ(x1+x2-2)
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенному множителю λ.
Составим систему:
∂L/∂x1 = 4x1+λ+x2+2 = 0
∂L/∂x2 = x1+λ+2x2-4 = 0
∂F/∂λ = x1+x2-2 = 0
Решаем данную систему с помощью формул Крамера.
Запишем систему в виде:
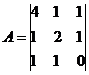
BT = (-2,4,2)
Главный определитель:
∆ = 4 · (2 · 0-1 · 1)-1 · (1 · 0-1 · 1)+1 · (1 · 1-2 · 1) = -4 = -4
Заменим 1-ый столбец матрицы А на вектор результата В.
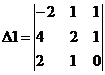
Найдем определитель полученной матрицы.
∆1 = -2 · (2 · 0-1 · 1)-4 · (1 · 0-1 · 1)+2 · (1 · 1-2 · 1) = 4
![]()
Заменим 2-ый столбец матрицы А на вектор результата В.
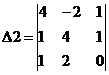
Найдем определитель полученной матрицы.
∆2 = 4 · (4 · 0-2 · 1)-1 · (-2 · 0-2 · 1)+1 · (-2 · 1-4 · 1) = -12
![]()
Заменим 3-ый столбец матрицы А на вектор результата В.
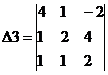
Найдем определитель полученной матрицы.
∆3 = 4 · (2 · 2-1 · 4)-1 · (1 · 2-1 · (-2))+1 · (1 · 4-2 · (-2)) = 4
![]()
Стационарная точка: F(-1; 3).
Пример №6. Найдем экстремум функции F(X) = x1·x2, используя функцию Лагранжа: L(X, λ)=F(X)+∑λi·φi(X).
Примечание: решение ведем с помощью сервиса Функция Лагранжа онлайн
