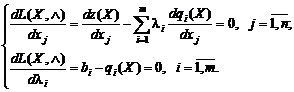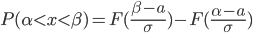Метод множителей Лагранжа
Приведенные выше условия оптимальности (теорема 5), лежат в основе метода множителей Лагранжа. который позволяет свести решение задачи (8) – (9) к решению задачи безусловной оптимизации ее функции Лагранжа. Для этого следует выполнить следующие действия.
1. Составить функцию Лагранжа по формуле (10).
2. Найти стационарные точки функции Лагранжа. Для этого нужно выписать частные производные по всем переменным xj и λi и приравнять их к нулю. Получается система n + m уравнений, представленная формулами (11) – (12). Все ее решения являются стационарными точками функции Лагранжа.
3. Любое решение (x*, λ*) системы (11) – (12) определяет точку x*, которая может быть локальным оптимумом ЦФ в задаче (8) – (9). Поэтому, найдя все решения системы (11) – (12), мы получим все точки, в которых ЦФ может иметь локальный оптимум.
4. Среди этих точек после дополнительного анализа отбираются такие, которые действительно являются точками локального оптимума. После сравнения значений ЦФ в этих точках находится точка, являющаяся глобальным оптимумом.
Следует иметь в виду, что если (х*, λ*) — стационарная точка функции Лагранжа, то не обязательно точка х* — локальный оптимум задачи (8) – (9). Это верно лишь тогда, когда исходная задача является задачей ВП. Более того, в этом случае х* — точка глобального оптимума этой задачи. Справедлива следующая теорема.
Теорема 6. Предположим, что задача (8) – (9) является задачей ВП, т.е. все ее ограничения линейные и ищется минимум выпуклой (максимум вогнутой) функции. Тогда, если (х*, λ*) — решение системы (11) – (12), то х* — точка глобального оптимума задачи (8) – (9).
Обобщенный метод множителей Лагранжа.
Для решения задачи (14) – (15) можно использовать обобщенный метод множителей Лагранжа. Основная идея этого метода заключается в последовательном учете ограничений. Предположим для определенности, что решается задача максимизации ЦФ.Сначала все ограничения отбрасываются, и решается задача безусловной максимизации ЦФ. Находится ее стационарная точка и проверяется ее допустимость. Если оказалось, что эта точка принадлежит ОДР, то процесс вычислений завершается, так как в силу выпуклости задачи (14) – (15) найденная точка является ее решением.
Если же найденная точка не допустима, то формируется новая задача, которая состоит в максимизации ЦФ с учетом первого ограничения задачи. Однако это ограничение записывается не как неравенство, а как равенство.
Получаем классическую задачу условной оптимизации вида:
Z = f (x1,…, xn) → mах,
g1(x1,…, xn) = b1.
Для ее решения используется метод множителей Лагранжа. Выписывается функция Лагранжа
L(x1,…, xn, λ) = f(x1,…, xn) + λ(b1 – g1 (x1,…, xn))
и решается система уравнений, определяющая стационарные точки этой функции:
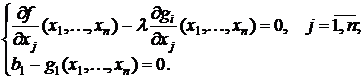
Если в результате получен вектор решения (x1*, ... , xn*, λ*) такой, что вектор (x1*, ... , xn*) допустим в исходной задаче и λ* ≥ 0, то это означает, что (x1*, ... , xn*) — искомая точка оптимума. Если же оказалось, что λ* < 0 или вектор (x1*, ... , xn*) недопустим в исходной задаче, то вместо первого ограничения берется второе ограничение и рассматривается задача
Z = f(x1,…, xn) → mах,
g2(x1,…, xn) = b2.
Эта задача также решается методом множителей Лагранжа. Если ее решение опять не является точкой оптимума исходной задачи, то берется третье ограничение и т.д. Если последовательный перебор отдельных ограничений не приводит к желаемому результату, то рассматриваются задачи с двумя ограничениями, затем тремя ограничениями и так до тех пор, пока не будет найдено оптимальное решение исходной задачи.
Замечание. Если исходная задача содержит ограничения типа равенства, то их нужно включать во все формируемые задачи.
На практике метод множителей Лагранжа применяется в различных областях. Например, для отыскания минимальных издержек (пример).
Метод неопределенных множителей Лагранжа
Пусть задача состоит в отыскании плана X, доставляющего экстремальное значение целевой функцииmax(min): Z = z(X) (1)
при ограничениях
qi(X) = bi, i = 1..m (2)
Будем считать, что функции (1) – (2) непрерывны и дважды дифференцируемые по своим аргументам. Как можно решить такую задачу условной оптимизации? Рассмотрим случай, когда число переменных равно двум и число ограничений – одному:
max(min): Z = z(x1,x2), (3)
q(x1,x2) = b. (4)
Выразим переменную x 2 в уравнении (4), получим выражение
x2 = φ(x1). (5)
Подставим его в целевую функцию (3). Получим
Z = z(x1, φ(x1)) (6)
как неявную функцию от переменной x 1. Необходимым условием существования экстремума функции (6), включающей исходное ограничение (4), является условие
или
Продифференцируем (4) по x1 как неявную функцию
Так как x2 = φ(x1), имеем
Подставим (9) в (8), получим
Обозначив
получим из (10), (11), (4) систему уравнений:
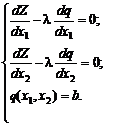
| (12) |
Для задачи в общем виде (1) – (2) функция Лагранжа будет иметь вид:
где (x1, ... , xn), Λ=(λ1, ... , λm)
Исходная задача (1) – (2) отыскания условного экстремума заменяется задачей отыскания безусловного экстремума функции Лагранжа L(X, λ), которая может быть решена через систему уравнений:
| (13)(14) |
Пример. Исследовать точки на экстремум Z=x1²+x2²; x1+x2=1
Составим функцию Лагранжа: L(x1, x2, λ) = x1²+x2² + λ(1-x1-x2)
Составим необходимые условия существования экстремума
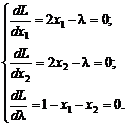
Решим систему уравнений
2x1-2x2-2λ=0,
2(x1+x2)=2λ, а т.к. x1+x2=1, то λ=1, тогда x1=½, x2=½.
Значение целевой Z=(½)²+(½)² = ½
Чтобы оценить, является ли точка экстремальной и какой экстремум она дает, обратимся к достаточному условию существования экстремума функции двух переменных (условию Лежандра-Клебша.
Составим определитель
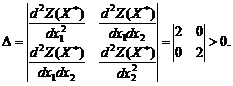
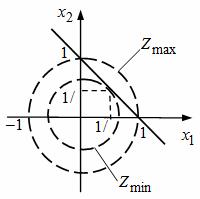
Рис. 2 - Графическое решение
Так как d2Z(X*) ⁄ dx12>0 и Δ>0, то в точке X*(½; ½) функция Z достигает минимальное значение. Графическое решение (рис. 2) показывает, что максимальное значение Zmax=1 достигается в точках (x1=1; x2=0) и (x1=0; x2=1) Таким образом, если бы исходная задача в примере ставилась бы на отыскание максимума, то с помощью решения системы уравнений необходимых условий существования экстремума мы точку максимума бы не определили. Требуется иной подход, который рассмотрим ниже в других разделах.