Теорема Куна-Таккера
Пусть дана задача нелинейного программирования| max: Z= z(X) | (1) |
| qi (X) ≤ bi, i = 1.. m | (2) |
| xj ≥0, j = 1.. n | (3) |
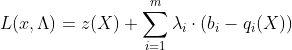(4)
где λi, i=1..m – неопределенные множители Лагранжа; z(X) и qi(X)– выпуклые вверх функции.
Теорема Куна-Таккера. Чтобы план X0 был решением задачи (1) – (4) необходимо и достаточно, чтобы существовал вектор λ0 ≥ 0 такой, что пара (X0,λ0) для всех X ≥ 0 и λ ≥ 0.
L(X, λ0) ≤ L(X0 ,λ0) ≤ L(X0 ,λ)
Назначение сервиса. Онлайн-калькулятор используется для нахождения экстремума функции через множители Лагранжа в онлайн режиме с проверкой решения в MS Excel. При этом решаются следующие задачи:
- составляется функция Лагранжа L(X) в виде линейной комбинации функции F(X) и ограничений gi(x);
- находятся частные производные функции Лагранжа, ∂L/∂xi, ∂L/∂λi;
- составляется система из (n+m) уравнений, ∂L/∂xi = 0.
- определяются переменные xi и множители Лагранжа αi.
Чтобы функция двух векторных переменных (4) имела седловую точку, необходимо и достаточно выполнения следующих условий Куна-Таккера:
(5)
(6)
(7)
(8)
Если решается задача минимизации, то имеет место седловая точка (X0, Y0), если выполняются соотношения
L(X, λ0) ≤ L(X0, Y0) ≤ L(X0, Y)
Условия же Куна-Таккера существования седловой точки функции Лагранжа поменяют знак в (5) и (7) на противоположный.
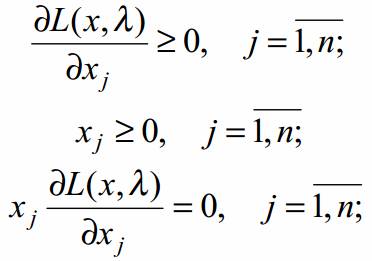
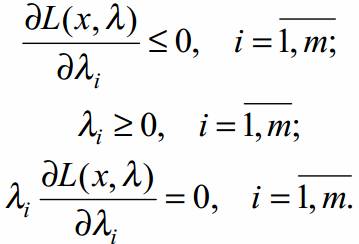
По содержанию условия Куна-Таккера (5)–(8) эквивалентны условиям второй теоремы двойственности задач линейного программирования.
Графически условия Куна-Таккера можно определить следующим образом.
- Изобразить допустимое множество и линии уровня целевой функции.
- Проверить выполнение условий Куна-Таккера в угловых точках допустимого множества (т.е. в точках, в которых число активных ограничений не меньше числа переменных) и в точках касания линии уровня целевой функции с границами допустимой области.
Пример №1. Проверить выполнение условий Куна-Таккера. Найти точку оптимума задачи линейного программирования с ограничениями:
f(x) = x12-x2 → min
g1(x) = x1 - 1 ≥ 0
g2(x) = 26 - x12-x22 ≥ 0
h1(x) = x1+x2 - 6 = 0
Решение:
Функция Лагранжа: L(X, λ) = x12-x2 - λ1(1-x1) + λ2(26-(x12+x22)) + λ3(6-(x1+x2))
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенным множителям λ.
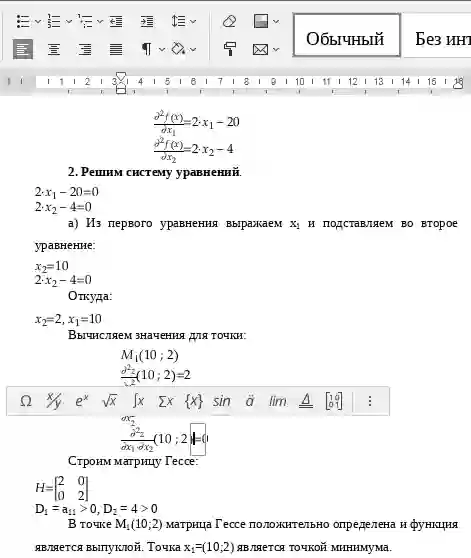
Проверим выполнение условий Куна-Таккера. Вычислим матрицы вторых производных целевой функции и функций ограничений.
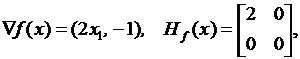
Матрица Гессе Hf положительно полуопределена при всех значениях x, следовательно f(x) – выпуклая функция.
Ограничение g1(x) – линейная функция, которая одновременно является выпуклой и вогнутой.
Матрица Гессе для функции g2(x) имеет вид:
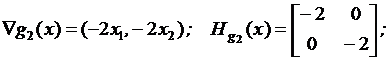
Так как матрица Hg2 отрицательно определена, то g2(x) является вогнутой.
Функция h1(x) входит в линейное ограничение в виде равенства. Следовательно, условия (а), (б) и (в) Теоремы 1 выполнены. Найдем теперь точку оптимума x*.
Имеем:
f(x)=x12-x2; ▽f(x)=(2x1,-1)
g1(x)=x1-1; ▽g1(x)=(1,0)
g2(x)=26-x12-x22; ▽g2(x)=(-2x1,-2x2)
h1(x)=x1+x2; ▽h1(x)=(1,1)
Уравнение принимает следующий вид:
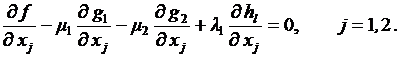
j=1, 2x1-μ1 + 2x2μ2 + λ1 = 0
j=2, -1 + 2x2μ2 + λ1 = 0
Таким образом, условия Куна-Таккера для нашего примера имеют следующий вид:
2x1-μ1 + 2x2μ2 + λ1 = 0
-1 + 2x2μ2 + λ1 = 0
x1 + x2 – 6=0
μ1(x1-1) = 0
μ2(26 - x12 – x22) = 0
μ1, μ2 ≥ 0
Из третьего уравнения находим: x1 = 6-x2. Подставив значение x1 в остальные уравнения, получим:
2(6-x2) - μ1 + 2μ2(6-x2)
-1 + 2x2μ2 + λ1 = 0
μ1(6-x2 -1) = 0 → x2 = 5, x1 = 1
μ2(26 – (6-x2)2 – x22) = 0
Подставим x2 = 5 в первое и второе уравнения:
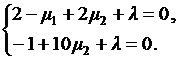
Из второго уравнения выразим λ и подставим в первое уравнение:
3 - μ1 - 8μ2 = 0
Пусть μ1 = 0,1 ≥ 0, тогда μ2 = 2,2 ≥ 0. Таким образом, точка x*=[5;1] является точкой минимума.
Пример №2.
f(x) = (x1-1)2 + x22 → min
g1(x) = -x1 + x2/5 ≥ 0
Найти точку минимума x*.
Решение: Запишем условия Куна–Таккера для данной задачи:
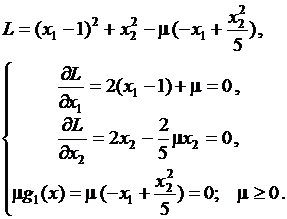
Из второго уравнения получим x2=0; подставим в третье уравнение, найдем x1=0. Тогда из первого уравнения следует μ=2. Таким образом, мы нашли точку x*=[0;0], которая может быть точкой минимума. Для этой точки ограничение g1(x*)=0, т. е. активно. Проверим выполнение условия: ▽g1(x*)=[-1; 2x2/5]|x2=0=[-1;0]. Условие будет выполнено для всех векторов y вида y=[0;y2]. Действительно, имеем:
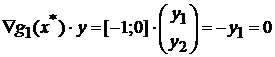, т. е. y1=0.
Матрица Гессе функции L в точке (x*, μ*) имеет вид:
,
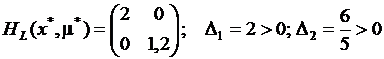т. е. матрица HL положительно определена и, следовательно, для любого вектора y≠0 имеем yTHL(x*,μ*)y>0, в том числе и для вектора вида y=[0;y2].
Таким образом, точка x*=[0;0] является точкой строгого локального минимума.
Заметим, что если мы воспользуемся необходимыми и достаточными условиями первого порядка, то не сможем дать заключение о том, что точка x*=[0;0] является решением задачи, так как не выполняется одно из условий теоремы – условие вогнутости функции g1(x).
Матрица Гессе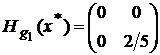 
не является отрицательно определенной, и поэтому g1(x) не является вогнутой.
Применение основной теоремы выпуклого анализа Куна–Таккера
Задание. По плану производства необходимо изготовит количество изделий, указанное в условии каждого задания «общий объём выпуска». Эти изделия могут быть изготовлены двумя технологическими способами. Стало известно, что при производстве х1 изделий первым способом затраты определяются функцией двух переменных х1, х2, соответствующей каждому варианту. При изготовлении х2 изделий вторым способом затраты также определяются функцией двух переменных х1, х2, соответствующей каждому варианту.Определить оптимальное число изделий, изготовленных различными способами, так чтобы общие затраты на производство продукции были минимальными (см. варианты заданий). Вычислить получаемую экономию от такого решения задачи.
Затраты для производства первым способом: x12 + 2 x1 руб.
Затраты для производства вторым способом: x22 + 16 x2 руб.
Общий объём выпуска: 100 шт.
Решение проводим с помощью калькулятора. Введём функцию суммарных затрат на производство f(x) и сформулируем математическую постановку задачи:
f(x)=x12+2x1+x22+16x2
при ограничении: x1+x2=197
Составляем функцию Лагранжа и задачу условной оптимизации сводим к задаче безусловной оптимизации: L(x, λ)=x12+2x1+x22+16x2-λ(x1+x2-197).
Находим первые частные производные функции Лагранжа и приравниваем их к нулю. Из полученной системы уравнений находим значения переменных х1, х2, возможно, соответствующие оптимальному решению исходной задачи.
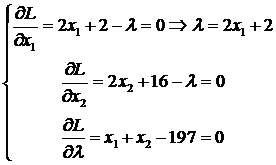
Подставляем выражение l через х1 во второе уравнение:
2x2+16-2x1-2=0 ⇒ 2x2-2x1+14=0 ⇒ x2=7+x1.
Полученное выражение для х2 подставляем в третье уравнение:
x1+7+x1-197=0 ⇒ x1=95, x2=7+95=102.
Проверяем, имеет ли исходная функция f(x) экстремум в точке (95; 102). Для этого вычисляем вторые частные производные f(x) и определитель, составленный из них: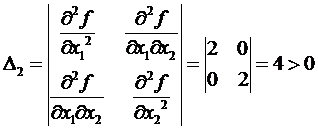 
. Следовательно, по теореме о достаточном условии существования экстремума функции нескольких переменных функция f(x) в точке имеет (95; 102) минимум, равный f(95, 102) = 952 + 2*95 + 1022 + 16*102 = 21251.
