Двойственность в линейном программировании

Основные определения теории двойственности.

Каждой задаче линейного программирования можно поставить в соответствие другую задачу линейного программирования. При решении одной из них автоматически решается и другая задача. Такие задачи называют взаимодвойственными. Покажем, как по данной задаче (будем называть ее исходной) построить двойственную ей.

Рассмотрим задачу о планируемом выпуске продукции.

F= 3х₁+ 5х₂+ 4х₃+ 5х₄→ max.
5x₁+0.4x₂+2x₃+0.5x₄≤400
5x₂+x₃+x₄≤300
x₁+x₃+x₄≤100
x₁≥0, x₂≥0, x₃≥0, x₄≥0

Содержательная постановка прямой задачи: составить такой план выпуска продукции X = (х₁,х₂ ..., х_n), при котором прибыль (выручка) от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов.

Общие правила составления двойственной задачи:

Прямая	Двойственная
Целевая функция (max)	Правая часть ограничений
Правая часть ограничений	Целевая функция (min)
A - матрица ограничений	A^T – матрица ограничений
`i`-ое ограничение: ≤ 0, (≥ 0)	Переменная y_i ≥ 0, (≤ 0)
`i`-ое ограничение: = 0	Переменная y_i≠ 0
Переменная x_j ≥ 0 (≤ 0)	`j`-ое ограничение: ≤ 0 (≥ 0)
Переменная x_j ≠ 0	`j`-ое ограничение: = 0

max → min

Прямая	Двойственная
Целевая функция (min)	Правая часть ограничений
Правая часть ограничений	Целевая функция (max)
A - матрица ограничений	A^T – матрица ограничений
`i`-ое ограничение: ≥ 0, (≤ 0)	Переменная y_i ≥ 0, (≤ 0)
`i`-ое ограничение: = 0	Переменная y_i≠ 0
Переменная x_j ≥ 0 (≤ 0)	`j`-ое ограничение: ≤ 0 (≥ 0)
Переменная x_j ≠ 0	`j`-ое ограничение: = 0

Построим двойственную ей задачу по следующим правилам.

Количество переменных в двойственной задаче равно количеству неравенств в исходной.
Матрица коэффициентов двойственной задачи является транспонированной к матрице коэффициентов исходной.
Столбец свободных членов исходной задачи является строкой коэффициентов для целевой функции двойственной. Целевая функция в одной задаче максимизируется, в другой минимизируется.
Условиям неотрицательности переменных исходной задачи соответствуют неравенства-ограничения двойственной, направленные в другую сторону. И наоборот, неравенствам-ограничениям в исходной соответствуют условия неотрицательности в двойственной.

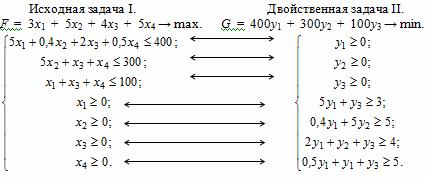
Заметим, что строки матрицы задачи I являются столбцами матрицы задачи II. Поэтому коэффициенты при переменных y_i в задаче II - это, соответственно, коэффициенты i-го неравенства в задаче I.
Полученная модель и есть экономико-математическая модель задачи, двойственной к прямой задаче.

Для построения двойственной задачи используйте этот сервис

Неравенства, соединенные стрелочками, будем называть сопряженными.
Содержательная постановка двойственной задачи: найти такой набор цен (оценок) ресурсов Y = (y₁, у₂ ..., у_m), при котором общие затраты на ресурсы будут минимальны при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли (выручки) от реализации этой продукции.
Цены ресурсов у₁, у₂ ..., у_m в экономической литературе получили различные названия: учетные, неявные, теневые. Смысл этих названий состоит в том, что это условные, «ненастоящие» цены. В отличие от «внешних» цен с₁, с₂ ..., с_n на продукцию, известных, как правило, до начала производства цены ресурсов у₁, у₂ ..., у_m являются внутренними, ибо они задаются не извне, а определяются непосредственно в результате решения задачи, поэтому их чаще называют оценками ресурсов.
Связь прямой и двойственной задач состоит, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой.

Теоремы двойственности

Двойственность является фундаментальным понятием в теории линейного программирования. Основные результаты теории двойственности заключены в двух теоремах, называемых теоремами двойственности.

Первая теорема двойственности.

Если одна из пары двойственных задач I и II разрешима, то разрешима и другая, причем значения целевых функций на оптимальных планах совпадают, F(x*) = G(y*), где х*, у* - оптимальные решения задач I и II

Вторая теорема двойственности.

Планы х* и у* оптимальны в задачах I и II тогда и только тогда, когда при подстановке их в систему ограничений задач I и II соответственно хотя бы одно из любой пары сопряженных неравенств обращается в равенство.
Это основная теорема двойственности. Другими словами, если х* и у* - допустимые решения прямой и двойственной задач и если c^Tx*=b^Ty*, то х* и у* – оптимальные решения пары двойственных задач.

Третья теорема двойственности. Значения переменных y_i в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов b_i системы ограничений - неравенств прямой задачи на величину целевой функции этой задачи:
Δf(x) = b_iy_i

Решая ЗЛП симплексным методом, мы одновременно решаем двойственную ЗЛП. Значения переменных двойственной задачи y_i, в оптимальном плане называют объективно обусловленными, или двойственными оценками. В прикладных задачах двойственные оценки y_i часто называются скрытыми, теневыми ценами или маргинальными оценками ресурсов.

Свойство взаимно двойственных задач

В одной задаче ищут максимум линейной функции, в другой — минимум.
Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой.
Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида ≤, а в задаче минимизации все неравенства вида ≥.
Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу:
Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
Условия неотрицательности переменных имеются в обеих задачах.

Итак, имеем исходную задачу I и ее оптимальное решение х* = (0, 40, 0, 100) и F(х*) = 700.

Применяя теорему двойственности, получим решение двойственной задачи по известному решению исходной задачи.
Найдем решение двойственной задачи II у* = (у₁, у₂, у₃), не прибегая к симплекс-методу, а воспользовавшись второй теоремой двойственности и известным оптимальным планом х*.

Рассмотрим выполнение неравенств задачи I при подстановке х* в систему ограничений.

5x₁+0,4x₂+2x₃+0,5x₄≤400	50+0,440+20 + 0,5100 = 66<400	Ограничение выполняется как строгое неравенство, т.е. ресурс 1-го вида израсходован не полностью. Значит, этот ресурс не является дефицитным и его оценка в оптимальном плане y₁ = 0.
5x₂+x₃+x₄≤300	5*40 + 0 + 100 = 300 = 300	Ограничение прямой задачи выполняется как равенство. Это означает, что 2-й ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y₂ ≠ 0)
x₁ + x₃ + x₄ ≤ 100	0 + 0 + 100 = 100 = 100	y₃ ≠ 0
x₁ ≥ 0	x₁ = 0	Первое ограничение в двойственной задаче будет неравенством 5y₁ + y₃ ≥ 3
x₂ ≥ 0	x₂ = 40 > 0	Второе ограничение в двойственной задаче будет равенством 0,4y₁ + 5y₂ = 5
x₃ ≥ 0	x₃ = 0	Третье ограничение в двойственной задаче будет неравенством 2y₁ + y₂ + y₃ ≥ 4
x₄ ≥ 0	x₄ = 100 > 0	Четвертое ограничение в двойственной задаче будет равенством 0,5y₁ + y₂ + y₃ = 5

Поскольку 1, 5, 7 неравенства строгие (имеют знак "<" или ">"), то соответствующие им неравенства в задаче II из пары сопряженных обязаны обратиться в равенства. имеем:
y₁=0
0.4y₁+5y₂=5
0.5y₁+y₂+y₃=5 или
y₁=0, y₂=1, y₃=4
т.е. у* = (0, 1, 4) - оптимальное решение.

Заметим, что действительно G(y*) = 400y₁+ 300y₂+ 100y₃= 400 · 0 + 300 · 1 + 100 · 4 = 700 = F(x*).

Итак, в силу второй теоремы двойственности мы очень быстро нашли оптимальное решение задачи II, пользуясь условием обращения в равенство хотя бы одного из пары сопряженных неравенств в системах ограничений двойственных задач.
Между переменными исходной задачи и переменными двойственной существует глубокая связь. А именно: после приведения обеих задач I и II к каноническому виду основные и дополнительные переменные задач соответствуют друг другу следующим образом:

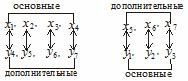
Установив такую связь, можно заметить, что, решив задачу I симплекс-методом и получив последнюю симплекс-таблицу (табл.), мы фактически решим и задачу II.
Запишем таблицу, учитывая соответствие между переменными х_i и y_j.

		у₄	у₂	у₆	у₃
	базисные	-х₁	-х₆	-х₃	-х₇	свободные
у₁	х₅					334
у₅	х₂					40
у₇	х₄					100
	-F	1	1	1	4	700

В силу соответствия и II теоремы двойственности переменные у₁, у₅, у₇ обязаны равняться 0, т.к. х₅, х₂, х₄>0 строго. А переменные у₄, у₂, у₆, у₃ принимают значения из индексной строки 1, 1, 1, 4 соответственно, т.к. им соответствующие переменные х₁, х₆, х₃, х₇ = 0, как свободные. Итак, из последней таблицы задачи II, не проводя даже никаких вычислений и пользуясь лишь соответствием переменных:

у* = (у₁*, у₂*, у₃*, у₄*, у₅*, у₆*, у₇*) = (0, 1, 4, 1, 0, 1, 0).

Мы научились по решению исходной задачи находить решение двойственной. Это оказалось возможно благодаря глубокой связи между переменными х_i и y_j. Осталось разобраться, каково экономическое содержание этих взаимосвязей.

Теорема равновесия

Задача 2
Составить двойственную задачу к задаче 1. Найти ее решение по теореме равновесия.
3x₁+x₂≥12
x₁+2x₂≥14
4x₁+11x₂≥68

Теорема равновесия. Пусть X*=(x₁*,...,x_n*) и Y*=(y₁*,...,y_n*) - допустимые планы пары двойственных задач в симметричной форме. Эти планы являются оптимальными тогда и только тогда, когда выполняются следующие условия дополняющей нежесткости:

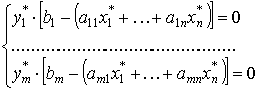
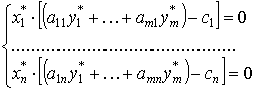
Теорема 4 позволяет определить оптимальное решение одной из пары двойственных задач по решению другой. Если ограничение одной задачи при подстановке оптимального решения обращается в строгое неравенство, то соответствующая двойственная переменная в оптимальном решении двойственной задачи равна 0. Если в оптимальном плане одной задачи какая-нибудь переменная положительна, то соответствующее ей ограничение двойственной задачи является уравнением.
Дадим экономическую интерпретацию условиям дополняющей нежесткости. Если в оптимальном решении какое-нибудь сырье имеет отличную от 0 оценку, то оно будет израсходовано полностью (ресурс является дефицитным). Если сырье расходуется не полностью (находится в избытке), то его оценка равна 0. Таким образом, получаем, что двойственные оценки – это мера дефицитности сырья. Оценка показывает, на сколько возрастет значение целевой функции при увеличении запаса соответствующего сырья на 1 ед. Если некоторый вид продукции входит в план производства, то затраты на его производство совпадают со стоимостью произведенной продукции. Если затраты на производство какого-нибудь вида продукции больше стоимости продукции, то продукция не производится.
В случае если одна из пары двойственных задач содержит две переменных, ее можно решить графически, а, затем, найти решение двойственной задачи, используя Теоремы 3 и 4. При этом могут возникнуть 3 случая: обе задачи имеют допустимые решения, допустимые решения имеет только одна задача, обе задачи не имеют допустимых решений.

Пример 2
Составить двойственную задачу и найти ее решение по теореме равновесия
x₂-2x₃+2x₄-2x₅≤4
-2x₁-2x₂+2x₃+2x₄+x₅≥2
x_i≥0, i=1,5
Z=10x₁-9x₂-19x₃-13x₄-11x₅ → max, если известно решение исходной задачи: Zmax=(3;4;0;0;0).
Построим двойственную задачу. Согласуем знаки неравенств с целью исходной задачи.

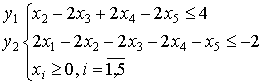
Z=10x₁-9x₂-19x₃-13x₄-11x₅ → max
Двойственная задача:

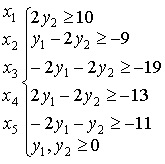
W=4y₁-2y₂ → min
Найдем оптимальное решение двойственной задачи по теореме равновесия. Запишем условия дополняющей нежесткости.
y₁(4-(x₂-2x₃+2x₄-2x₅))=0
y₂(-2-(2x₁-2x₂-2x₃-2x₄-x₅))=0
x₁(-2y₂-10)=0
x₂(y₁-2y₂+9)=0
x₃(-2y₁-2y₂+19)=0
x₄(2y₁-2y₂+13)=0
x₅(-2y₁-y₂+11)=0
Подставим в составленную систему оптимальное решение исходной задачи: x₁=3, x₂=4, x₃=0, x₄=0, x₅=0.
y₁(4-(4-2·0+2·0-2·0))=0
y₂(-2-(2·3-2·4-2·0-2·0-0))=0
3·(-2y₂-10)=0
4·(y₁-2y₂+9)=0
0·(-2y₁-2y₂+19)=0
0·(2y₁-2y₂+13)=0
0·(-2y₁-y₂+11)=0
Произведение равно нулю, если один из множителей равен 0. Получаем
y₁·0=0
y₂·0=0
2y₂-10=0
y₁-2y₂+9=0
0=0
0=0
0=0
Тогда,
-2y₂-10=0
y₁-2y₂+9=0
или
y₂=5, y₁=2y₂+9 = 10-9=1
Оптимальное решение двойственной задачи Wmin=W(1;5). По Теореме 3 Zmax=Wmin= -6. Окончательно, Wmin=W(1;5)=-6.

Пример 3
Составить двойственную задачу к задаче из примера раздела 1.5 и найти ее решение по теореме равновесия
x₁+3x₂≥12
5x₁+4x₂≥31
2x₁+3x₂≥18
x₁, x₂≥0
Z(x₁,x₂)=12000x₁+16000x₂→min
В разделе 1.5 было найдено решение исходной задачи средствами MS Excel: Zmin(3;4)=100000
Составим двойственную задачу. Знаки неравенств уже согласованы с целью задачи.

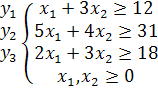
Z(x₁,x₂)=12000x₁+16000x₂→min
Двойственная задача:

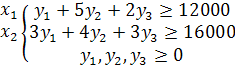
W(y₁, y₂, y₃)=12y₁+31y₂+18y₃ → max
Найдем оптимальное решение двойственной задачи по теореме равновесия. Запишем условия дополняющей нежесткости.
y₁(x₁+3x₂-12)=0
y₂(5x₁+4x₂-31)=0
y₃(2x₁+3x_{2x₁(12000-(y₁+5y₂+2y₃))=0

x₂(16000-(3y₁+4y₂+3y₃))=0}

Подставим в составленную систему оптимальное решение исходной задачи: x₁=3, x₂=4.
y₁(3+3·4-12)=0
y₂(5·3+4·4-31)=0
y₃(2·3+3·4-18)=0
3·(12000-(y₁+5y₂+2y₃))=0
4·(16000-(3y₁+4y₂+3y₃))=0
Произведение равно нулю, если один из множителей равен 0. Получаем
y₁·3=0, y₁=0
y₂·0=0
y₃·0=0
12000-(y₁+5y₂+2y₃)=0
16000-(3y₁+4y₂+3y₃)=0
Тогда,
12000-(0+5y₂+2y₃)=0
16000-(3·0+4y₂+3y₃)=0
или
5y₂+2y₃=12000 | × 3
4y₂+3y₃=16000 | × 2
или
15y₂+6y₃=36000
8y₂+6y₃=32000

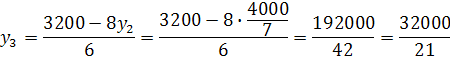
Вычтем из первого уравнения второе:
,

Оптимальное решение двойственной задачи . По Теореме 3 Zmax=Wmin=100000.
Окончательно, Wmin=W(0; 4000/7; 32000/21) = 100000