Экономическая интерпретация двойственной задачи и теории двойственности
Рассмотрим экономическую интерпретацию двойственности на примере задачи оптимального использования сырья.Исходная задача I имела конкретный экономический смысл: основные переменные хi обозначали количество произведенной продукции i-го вида, дополнительные переменные обозначали количество излишков соответствующего вида ресурсов, каждое из неравенств выражало собой расход определенного вида сырья в сравнении с запасом этого сырья. Целевая функция определяла прибыль при реализации всей продукции. Предположим теперь, что предприятие имеет возможность реализовывать сырье на сторону. Какую минимальную цену надо установить за единицу каждого вида сырья при условии, чтобы доход от реализации всех его запасов был не меньше дохода от реализации продукции, которая может быть выпущена из этого сырья.
Экономико-математический анализ решений. Сформулируем экономические выводы на примере пары двойственных задач, приведенных выше:
- для любого допустимого плана производства X и любого допустимого вектора оценки ресурсов Y общая созданная стоимость не превосходит суммарной оценки ресурсов;
- если задача определения оптимального плана, максимизирующего выпуск продукции разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученная при реализации оптимального плана совпадает с суммарной оценкой ресурсов.
Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, т.е. равенство общей оценки продукции и ресурсов, и обуславливают убыточность всякого другого плана, отличного от оптимального; - если по некоторому оптимальному плану X* производства расход i-го ресурса строго меньше его запаса Ьъ то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок Y* его j-ая компонента строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Значит, двойственные оценки могут служить мерой дефицитности ресурса;
- двойственные оценки ресурсов показывают, на сколько денежных единиц изменится максимальная прибыль от реализации продукции при изменении запаса соответствующего ресурса на одну единицу.
Одно из эффективных средств экономико-математического анализа - использование двойственных оценок оптимального плана, которые выступают:
- как мера дефицитности ресурсов и продукции;
- как мера влияния ограничений на целевую функцию;
- как инструмент определения эффективности отдельных вариантов;
- как инструмент балансирования затрат и результатов.
Переменные у1, у2, у3 будут обозначать условную предполагаемую цену за ресурс 1, 2, 3 вида соответственно. Тогда доход от продажи видов сырья, расходуемых на производство одной единицы продукции I, равен: 5у1 + 1· у3. Т.к. цена продукции I типа равна 3 ед., то 5у1 + у3 ≥ 3, в силу того, что интересы предприятия требуют, чтобы доход от продажи сырья был не меньше, чем от реализации продукции. Именно в силу такого экономического толкования система ограничений двойственной задачи принимает вид:
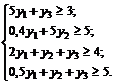
А целевая функция G = 400y1 + 300y2 + 100y3 подсчитывает условную суммарную стоимость всего имеющегося сырья. Понятно, что в силу I теоремы двойственности F(x*) = G(y*) равенство означает, что максимальная прибыль от продажи всей готовой продукции совпадает с минимальной условной ценой ресурсов. Условные оптимальные цены уi показывают наименьшую стоимость ресурсов, при которой выгодно обращать эти ресурсы в продукцию, производить.
Еще раз обратим внимание на то, что уi - это лишь условные, предполагаемые, а не реальные цены на сырье. Тот факт, что у1* = 0 вовсе не означает, что реальная цена первого ресурса нулевая. Равенство нулю условной цены означает лишь, что этот ресурс не израсходован полностью, имеется в излишке, недефицитен. Действительно, посмотрим на первое неравенство в системе ограничений задачи I, в котором подсчитывается расход первого ресурса: 5х1* + 0,4х2* + 2х3* + 0,5х4* = 66 < 400. его избыток составляет х5 = 334 ед. при данном оптимальном плане производства. Этот ресурс имеется в избытке, и поэтому для производителя он недефицитен, его условная цена равна 0, его не надо закупать. Наоборот, ресурс 2 и 3 используются полностью, причем у3 = 4 а у2 = 1, т.е. сырье третьего вида более дефицитно, чем второго, его условная цена больше. Если производитель продукции имел бы возможность приобретать дополнительно сырье к уже имеющемуся, с целью получения максимального дохода от производства, то увеличив сырье второго вида на единицу, он бы получил дополнительно доход в у2 денежных единиц, с увеличением на единицу сырья третьего вида, значение целевой функции увеличилось бы еще на у3 единицы.
Если перед производителем стоит вопрос, "выгодно ли производить какую-либо продукцию при условии, что затраты на единицу продукции составят 3, 1, 4 единиц 1, 2, 3-го видов сырья соответственно, а прибыль от реализации равна 23 единицам", то в силу экономического истолкования задачи ответить на этот вопрос несложно, поскольку затраты и условные цены ресурсов известны. Затраты равны 3, 1, 4, а цены у1* = 0, у2* = 1, у3* = 4. Значит, можно посчитать суммарную условную стоимость ресурсов, необходимых для производства этой новой продукции: 3 · 0 + 1 · 1 + 4 · 4 = 17 < 23. значит продукцию производить выгодно, т.к. прибыль от реализации превышает затраты на ресурсы, в противном случае ответ бы на этот вопрос был отрицательным.
Ответим на вопрос, как изменится целевая функция в оптимальном плане, если цену первого вида продукции увеличить до 20?
Оценка y1=0, ресурс не дефицитен, и оптимальный план X не изменится: ΔFmax=Δc1*x1=(20-3)*0=0
В данном случае, значение целевой функции не изменилось, поскольку в оптимальном плане x1=0.
Анализ решения задачи линейного программирования с помощью теории двойственности
Математическая модель является прекрасным средством получения ответов на широкий круг самых разнообразных вопросов, возникающих при принятии оптимальных решений. Виды анализа, выполняемого на основе математической модели, приведены на рисунке.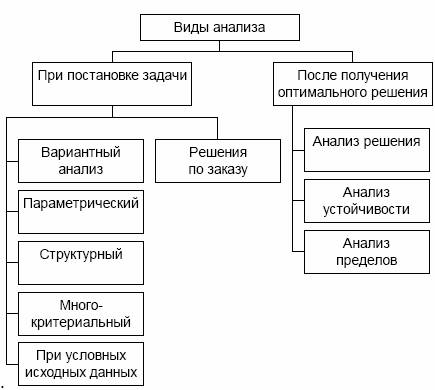
Двойственность в задачах линейного программирования
Теория двойственности представляет собой весьма важное, как с чисто теоретической, так и с практической точки зрения, направление математического программирования. Основной идеей теории двойственности является то, что для каждой задачи линейного программирования (ЛП) существует некоторая задача ЛП, решение которой тесно связано с решением прямой. Между решениями прямой и двойственной задач имеется ряд важных соотношений, полезных при исследовании общих свойств оптимального решения задач ЛП и проверке оптимальности допустимого решения.Рассмотрим задачу: найти min f(x), x Є Rn (1)
при ограничениях gj( x)≤ 0, j = 1, m; m<n.
Эту задачу называют прямой. Существует связанная с ней задача максимизации, называемая двойственной:
L(x,λ) = max
где L(x,λ) – функция Лагранжа.
Понятие двойственности устанавливает определенные отношения между решениями прямой и двойственной задач.
Определение. Две экстремальные задачи называются эквивалентными, если множества их решения совпадают, либо обе задачи не имеют решений.
Двойственность
Теория двойственности представляет собой фундаментальное понятие в математическом программировании, имеющее теоретическое и практическое значение.Основная идея теории двойственности: для каждой задачи ЛП существует некоторая задача ЛП, решение которой тесно связано с прямой. Между решениями прямой и двойственной задач имеется ряд важных соотношений, полезных при исследовании общих свойств оптимального решения ЗЛП и проверке оптимальности допустимого решения.
Двойственная задача к ЗЛП в стандартной форме: рассмотрим ЗЛП (в стандартной форме)
min Z = C*X,
A*X = B,
X ≥ 0
(П) Прямая задача.
Каждому i–му (i = 1,m) ограничению поставим в соответствие переменное ui, положительное, отрицательное или нуль (называемое двойственным переменным), и рассмотрим ЗЛП.
max W = U*B
U* AT ≤ C, AT*U ≤ C
(Д) Двойственная задача
где U есть, так называемый, вектор–строка (u1, u2, …, um).
Линейная задача (Д) тесно связана с линейной задачей (П):
- матрица ограничений (Д) есть транспонированная матрица задачи (П);
- вектор "цен"
Данная таблица соответствий между прямой и двойственной задачами позволяет записать непосредственно двойственную задачу для любой линейной задачи.
Таблица
| Прямая | Двойственная |
| Целевая функция (min) | Правая часть ограничений |
| Правая часть ограничений | Целевая функция (max) |
| A – матрица ограничений | AT– матрица ограничений |
| i–ое ограничение: ≥ 0, (≤0) | Переменная ui≥ 0, (≤0) |
| i–ое ограничение: = 0 | Переменная ui≠ 0 |
| Переменная x ≥ 0 | j–ое ограничение: ≤ 0 |
| Переменная x ≠ 0 | j–ое ограничение: = 0 |
Замечание: двойственная к двойственной задаче совпадает с прямой.
Пример
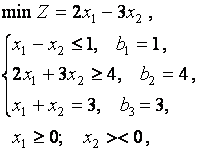
т.е. вторая переменная не ограничена по знаку, она может быть как больше 0, так и меньше 0.
Построим двойственную задачу. Так как число ограничений равно трем, то имеем три переменных: u1, u2, u3. ЦФ задачи (Д) имеет вид:
max W = U*B = u1b1 + u2b2 + u3b3 = u1 + 4u2 + 3u3
В прямой задаче имеем матрицу А: .
В задаче (Д) имеем транспонированную матрицу: .
Таким образом, двойственная задача выглядит так:
max W = u1 + 4u2 + 3u3

Теорема двойственности. Если X и U - соответственно допустимые решения произвольных прямой и двойственной задач, то Z = C*X ≥ W = U*B.
Следствие из теоремы. Если X*, U* - соответственно решения прямой и двойственной задач, удовлетворяющих равенству C*X* = U*B, то планы X* и U*– оптимальные решения прямой и двойственной задач соответственно.
Теорема. Пусть заданы прямая и двойственная задачи:
а) если прямая и двойственная задачи имеют решения, то каждая из этих задач имеет оптимальное решение и
Z* = min(П) = max(Д) = W*
б) если одна из них имеет неограниченный оптимум, то другая не имеет решения.
Теорема. Два решения (X и U) соответственно прямой и двойственной задач оптимальны тогда и только тогда, если выполняется условие:
(U* Aj - cj)*xj = 0; j = 1, n, где Aj – j–й столбец матрицы A.
Поясним некоторые вопросы. На этапе постановки задачи производится анализ с целью ответить на вопросы: «Что будет, если…?» и (или) «Что надо, …, чтобы …?». Анализ с целью ответа на первый вопрос называется вариантным анализом, на второй – решениями по заказу.
Вариантный анализ бывает следующих видов: Параметрическим будем называть такой анализ, который заключается в решении задачи при различных значениях некоторого параметра; Под структурным анализом будем понимать решение задачи оптимизации при различной структуре ограничений; Многокритериальный анализ – это решение задачи по разным целевым функциям; Если исходные данные, используемые при решении задачи, зависят от соблюдения дополнительных условий, то такой анализ называется анализом при условных исходных данных.
Во вторую группу – решения по заказу – входят задачи, целью которых является решение задачи оптимизации при заданных значениях: переменных, левых частей ограничений, целевой функции.
Кроме анализа, выполняемого на этапе постановки задачи, мощным средством, помогающим принять решение, является анализ полученного оптимального плана.
Вопросы для самоконтроля
- Для каждой ли задачи ЛП существует двойственная?
- Как связаны прямая исходная и двойственная задачи?
- Что такое сопряженные ограничения?
- Сформулируйте теоремы двойственности.
- Каков экономический смысл дополнительных переменных в исходной задаче?
- Каков экономический смысл основных переменных в двойственной задаче?
- Как изменится значение целевой функции, если запас i-го ресурса увеличить на единицу?
