Одноканальные системы массового обслуживания
Назначение сервиса СМО. Онлайн-калькулятор предназначен для расчета следующих показателей одноканальных СМО:- вероятность отказа канала, вероятность свободного канала, абсолютная пропускная способность;
- относительная пропускная способность, среднее время обслуживания, среднее время простоя канала.
см. также Многоканальные модели систем массового обслуживания: Многоканальная СМО с отказами в обслуживании, Многоканальная СМО с ограниченной длиной очереди (СМО с ожиданием), Многоканальная СМО с неограниченной очередью. Системы массового обслуживания. Примеры решений
Классификация одноканальных систем массового обслуживания
- Одноканальная СМО с отказами в обслуживании:
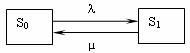
- Одноканальная СМО с ограниченной длиной очереди:

- Одноканальная СМО с неограниченной очередью
Пример №1. Авто заправочная станция имеет одну бензоколонку. Предполагается что простейший поток автомашин поступает на станцию с интенсивностью λ=11 автомашин/ч. Время обслуживания заявки случайная величина которая подчиняется экспоненциальному закону с параметром μ=14 автомашин/ч. Определить среднее число автомашин на станции.
Пример №2. Имеется пункт проведения профилактического осмотра машин с одной группой проведения осмотра. На осмотр и выявление дефектов каждой машины затрачивается в среднем 0,4 часа. На осмотр поступает в среднем 328 машин в сутки. Потоки заявок и обслуживаний - простейшие. Если машина, прибывшая в пункт осмотра не застает ни одного канала свободным, она покидает пункт осмотра необслуженной. Определить предельные вероятности состояний и характеристики обслуживания пункта профилактического осмотра.
Решение. Здесь α = 328/24 ≈ = 13.67, t = 0.4. Эти данные необходимо ввести в калькулятор.




