Многоканальные системы массового обслуживания

• вероятность отказа канала, вероятность свободного канала, абсолютная пропускная способность;
• относительная пропускная способность, среднее время обслуживания, среднее время простоя канала.

Инструкция. Для решения подобных задач в онлайн режиме выберите модель СМО. Укажите интенсивность потока заявок λ и интенсивность потока обслуживания μ. Для многоканальной СМО с ограниченной длиной очереди можно указать длину очереди m, а для многоканальной СМО с неограниченной очередью - число заявок в очереди (для расчета вероятности нахождения этих заявок в очереди). Полученное решение сохраняется в файле Word (см. Системы массового обслуживания. Примеры решений). Подробнее как заполнять данные.

• Ввод данных
• Инструкция
• Оформление Word

Пример №1. В типографию с тремя множительными аппаратами поступают заказы от соседних предприятий на размножение рабочей документации. Если все аппараты заняты, то вновь поступающий заказ не принимается. Среднее время работы с одним заказом составляет 2 часа. Интенсивность потока – 0,5 заявки в час. Найти предельные вероятности состояний и показатели эффективности работы типографии.
Здесь: n = 3, Модель СМО: Многоканальная СМО с отказами в обслуживании, λ = 0,5 заявки в час, t_обс = 2 час.

Пример №2. Сколько автомобилей следует иметь на станции скорой помощи, если:

1. в среднем в час поступает 10 заявок (вызовов);
2. среднее продолжительность обслуживания одной заявки 1час 20 минут;
3. среднее время ожидания (время от момента вызова до момента выезда бригады) не должно превышать 5 минут.

см. также: Одноканальные модели систем массового обслуживания: Одноканальная СМО с отказами в обслуживании, Одноканальная СМО с ограниченной длиной очереди (СМО с ожиданием), Одноканальная СМО с неограниченной очередью.

Классификация многоканальных систем массового обслуживания

1. Многоканальная СМО с отказами в обслуживании.
   Система S (СМО) имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе): S₀, S₁, S₂, …, S_k, …, S_n, где S_k — состояние системы, когда в ней находится k заявок, т.е. занято k каналов.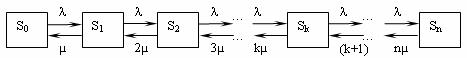
   
2. Многоканальная СМО с ограниченной длиной очереди.
   Система может находиться в одном из состояний S₀, S₁, S₂,…, S_k,…, S_n,…, — нумеруемых по числу заявок, находящихся в СМО: S₀ — в системе нет заявок (все каналы свободны); S₁ — занят один канал, остальные свободны; S₂ — заняты два канала, остальные свободны;..., S_k — занято k каналов, остальные свободны;..., S_n — заняты все n каналов (очереди нет); S_n+1 — заняты все n каналов, в очереди одна заявка;..., S_n+r — заняты все n каналов, r заявок стоит в очереди.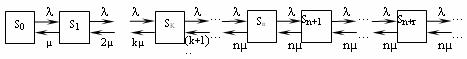
   
3. Многоканальная СМО с неограниченной очередью